64-точечное преобразование обеспечило лучшее качество распознавания: минимальная достижимая ошибка составляет 0,060 (Биортогональный-3.7) против 0,103 у 32-точечного преобразования (Биортогональный-1.5, -2.4, -2.6). Для преобразования Фурье результаты практически одинаковы в обоих случаях.
В группе фильтров Добеши лучшие результаты для 32 отсчетов—
у фильтров 1 и 7 (![]() ), для 64 отсчетов — у
фильтра 6 (
), для 64 отсчетов — у
фильтра 6 (![]() ).
).
В группе фильтров на основе койфлетов лучшие результаты для
32-отсчетных выборок — у фильтра 1 (![]() ), для
64-отсчетных — у фильтра 5 (
), для
64-отсчетных — у фильтра 5 (![]() ).
).
В группе фильтров на основе симлетов лучшие результаты для
32-отсчетных выборок — у фильтра 4 (![]() ), для
64-отсчетных — у фильтра 5 (
), для
64-отсчетных — у фильтра 5 (![]() ).
).
В группе фильтров на биортогональных вейвлетах лучшие
результаты для 32-отсчетных выборок — у фильтров 1.5, 2.4 и 2.6 (![]() ), для 64-отсчетных — у фильтра 3.7 (
), для 64-отсчетных — у фильтра 3.7 (![]() ).
).
В целом у группы биортогональных фильтров наилучшие показатели.
Непосредственная связь между коррелированностью спектральных составляющих и вероятностью правильного распознавания не прослеживается. Это видно при сопоставлении таблиц 9.1 и 9.2.
В реальных условиях сигнал всегда попадает на вход приемника вместе шумом, обычно аддитивным. При прохождении номального шума через линейный детектор его закон распределения не изменяется, меняются лишь спектр и, соответственно, корреляционная функция шума. Рассмотрим прохождение смеси сигнала и шума через линейный детектор с характеристикой, описываемой выражением
|
|
Пусть шум на входе детектора обладает заданной дисперсией и нулевым матожиданием. Процесс на выходе детектора будет иметь то же распределение и ту же дисперсию, что у входного шума, но каждый отсчет процесса будет сдвинут по амплитуде на величину входного полезного сигнала в точке, соответствующей данному отсчету. Плотность распределения процесса на выходе
|
|
где y — значение сигнала в данной точке, D — дисперсия шума.
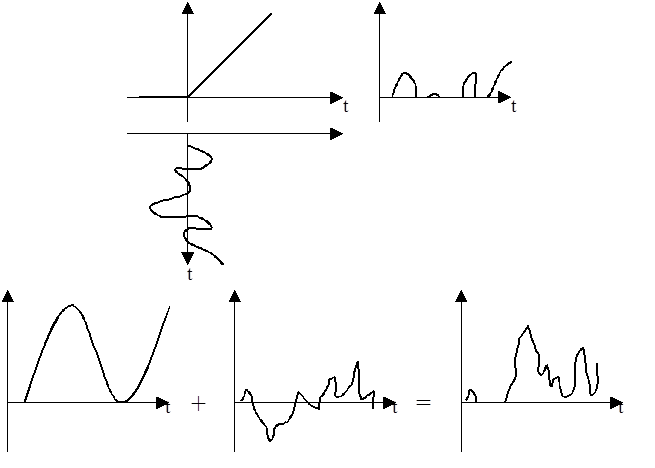
Рис. 9.14. Иллюстрация прохождения сигнала через линейный детектор
Кроме того, поскольку характеристика детектора такова, что сигналы отрицательной полярности не пройдут с входа на выход, вводится ограничение, согласно которому отсчеты отрицательной полярности приравниваются к нулю. Эти положения иллюстрируются рис. 9.12.
Прежде всего необходимо было получить достаточно хороший генератор нормально распределенных случайных чисел.
Для получения последовательностей нормально распределенных случайных чисел была применена методика, изложенная в [18]. Первоначально были исследованы различные способы получения равномерно распределенных в интервале [0,1) случайных чисел, но оказалось, что наилучшими параметрами (в соответствии с критерием Колмогорова) обладает системный (встроенный в язык С++) генератор, который и был использован в дальнейшем. В качестве начального значения для генератора в программе использовались данные системных часов (миллисекунды), поэтому число возможных начальных значений равно 1000, что достаточно для наших целей. Поскольку в генераторе используются 32-разрядные числа, то период повторения последовательности не хуже, чем у наихудшего в этом смысле метода, указанного в [18], то есть не менее 229, что, с учетом числа обрабатываемых сигналов, также достаточно для наших целей.
Для получения нормально распределенных случайных чисел с матожиданием 0 и дисперсией 1 были испробованы различные методы (обратной функции, а также специально разработанные для получения нормальных случайных чисел методы Бокса-Маллера и Марсальи-Грея). По результатам экспериментов лучшими параметрами обладали последовательности чисел, полученных в соответствии с центральной предельной теоремой по формуле
|
|
(9.9) |
при числе слагаемых ![]() . При увеличении
или уменьшении числа слагаемых распределение резко ухудшалось.
. При увеличении
или уменьшении числа слагаемых распределение резко ухудшалось.
Для проверки качества распределения был использован критерий
![]() Пирсона. Выборка объемом
Пирсона. Выборка объемом ![]() элементов разбивалась на
элементов разбивалась на ![]() интервалов и затем рассчитывалась
величина расхождения между экспериментальной и теоретической плотностями
распределения
интервалов и затем рассчитывалась
величина расхождения между экспериментальной и теоретической плотностями
распределения
|
|
(9.10) |
где ![]() — число попаданий случайной
величины Х в i-тый
интервал, а
— число попаданий случайной
величины Х в i-тый
интервал, а ![]() — теоретическая вероятность
попадания случайной величины Х в i-тый интервал.
— теоретическая вероятность
попадания случайной величины Х в i-тый интервал. ![]() рассчитывалось
исходя из известной плотности распределения нормальной случайной величины.
рассчитывалось
исходя из известной плотности распределения нормальной случайной величины.
Для выбранного способа получения величина ![]() колебалась в пределах 11…20 в
зависимости от начального значения генератора. По результатам ряда опытов было
получено среднее значение
колебалась в пределах 11…20 в
зависимости от начального значения генератора. По результатам ряда опытов было
получено среднее значение ![]() . Наглядно
расхождение между теоретическими требованиями и практической реализацией
показано на рис. 9.13 для значения
. Наглядно
расхождение между теоретическими требованиями и практической реализацией
показано на рис. 9.13 для значения ![]() при единичных
матожидании и дисперсии и объеме выборки
при единичных
матожидании и дисперсии и объеме выборки ![]() (здесь
через P(X) обозначено
теоретическое распределение, через P*(X) —
практические результаты).
(здесь
через P(X) обозначено
теоретическое распределение, через P*(X) —
практические результаты).
На распределение накладывается три независимых условия:
·
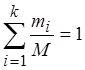 ;
;
·
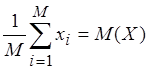 , то есть статистическая
оценка матожидания распределения должна совпадать с теоретическим матожиданием;
, то есть статистическая
оценка матожидания распределения должна совпадать с теоретическим матожиданием;
·
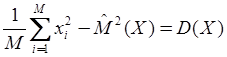 , то есть требуется
совпадение теоретической и статистической дисперсий.
, то есть требуется
совпадение теоретической и статистической дисперсий.
Следовательно, число степеней свободы ![]() . Из таблицы 1 в [18]
находим, что для
. Из таблицы 1 в [18]
находим, что для ![]() и
и ![]() вероятность
вероятность
![]() , то есть достаточно велика.
Следовательно, гипотезу о том, что величина
, то есть достаточно велика.
Следовательно, гипотезу о том, что величина ![]() распределена
по нормальному закону с заданными матожиданием и дисперсией можно считать не
противоречащей опытным данным.
распределена
по нормальному закону с заданными матожиданием и дисперсией можно считать не
противоречащей опытным данным.
Наконец, при помощи линейного преобразования
|
|
(9.11) |
при любом ![]() и
и ![]() получаем
последовательность случайных чисел
получаем
последовательность случайных чисел ![]() с распределением
с распределением ![]() из последовательности чисел
из последовательности чисел ![]() , распределенных в соответствии с
, распределенных в соответствии с ![]() .
.
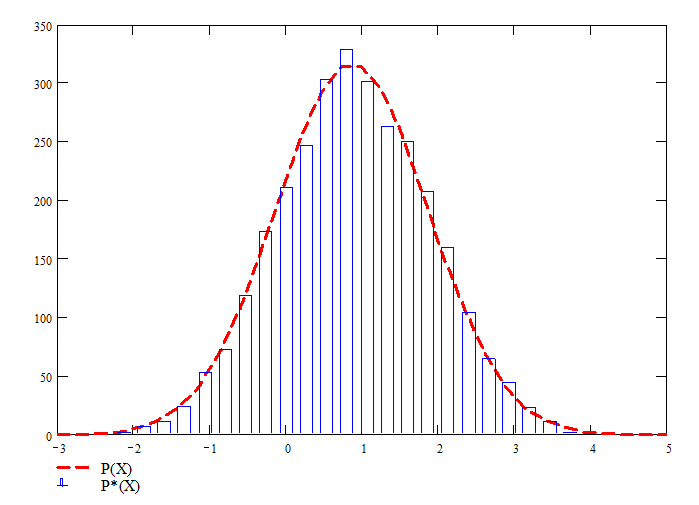
Рис. 9.15. Теоретический и экспериментальный графики плотности распределения нормальной случайной величины с единичными матожиданием и дисперсией
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.