Разработка программы анализа сигналов по критерию отношения правдоподобия, построенного с использованием вейвлет-спектров, страница 3

Эти результаты требуют некоторых пояснений. Как видно, эффективность преобразования в смысле декорреляции приблизительно одинакова. Следовательно, по этому признаку выбрать лучший базис невозможно.

При переходе от первой группы ко второй автокорреляция могла как возрастать, так и снижаться, в зависимости от базиса.

Теоретически, дополнение выборок до 64 отсчетов несколько увеличивает взаимозависимость спектральных составляющих. Практически это произошло только со спектрами в базисе Фурье; спектральные составляющие в вейвлет-базисах не только не стали в среднем более коррелированными, но, напротив, взаимозависимость ослабла. Это объясняется тем, что, поскольку у длинных выборок среди 64-отсчетов велико число нулевых, в спектрах также велико число именно нулевых коэффициентов (см п.3.3), причем фактически на одних и тех же позициях для всех выборок. Это приводит к тому, что в корреляционной матрице появляется большое количество нулевых составляющих и, как следствие, сильно уменьшается значение S, отнесенного к общему количеству элементов матрицы.

Поэтому выводы, диктуемые данными статистической обработки, требующей применения 64-точечного преобразования и отказа от 32-точечного в связи с явной большей коррелированностью коэффициентов последнего, неверны. Нулевые спектральные составляющие неинформативны, и не могут быть использованы при построении решающего правила, поэтому на этом этапе нельзя было оценить, какой базис и какая длина выборки дадут лучшие результаты.

9.4. Распознавание без шума

На данной стадии работы было проведено исследование эффективности базисов в задаче поиска и распознавания чистых сигналов, без шумов.

В качестве тестовых сигналов здесь и далее использовались те же выборки, что применялись для получения статистических параметров спектров. Вероятность ошибки

где апостериорная вероятность правильного распознавания (эффективность распознавания) 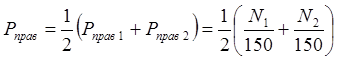. Здесь  — число правильно распознанных выборок первой группы,  — число правильно распознанных выборок второй группы. Результаты сведены в таблице 9.2.

Таблица 9.2. Распознавание сигналов без шума