Определение средний скорости движения, глубину равномерного движения воды в канале. Определение критической глубины и критического уклона в канале

Санкт-Петербургский Государственный

политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Задание №4

по курсу гидравлики

Студент:

группа 3012/1

                                          Преподаватель:

 Кожевникова Е.Н.

Санкт-Петербург

2005

Содержание

1.	Определить глубину равномерного движения ho1 и ширину канала по дну b на подводящем участке канала при β = (βг.н.)пред.
2.	Определить глубину равномерного движения на отводящем участке канала ho2, полагая ширину канала b, равной найденной в п.1
3.	Определить средние скорости движения воды в канале и сравнить их с максимально допустимыми для заданного грунта скоростями.
4.	При υ > υнеразм определить глубину наполнения и уклон дна канала, полагая  υ = υнеразм
5.	Определить критическую глубину hк и критический уклон iк
6.	Построить график удельной энергии сечения Э(h)
7.	Пользуясь способом Чарномского, постоить кривую свободной пов-ти на подводящем участке канала ( 1,05hO1 до hp)
8.	Построить кривые свободной поверхности на отводящем участке канала при условиях: а) открытие затвора е=0,3hк б) глубина воды в конце канала равна hk
9.	Построить кривую свободной поверхности на подводящем и отводящем участках канала при полностью открытом затворе
10.	Построить график прыжковой функции θ(h), совместив его с графиком удельной энергии сечения Э(h)
11.	Построить линию сопряженных глубин для кривой типа c1 и определить местоположение прыжка.
12.	Определить длину гидравлического прыжка и потери энергии в нем. Представить на рисунке схему гидравлического прыжка и показать на ней напорную линию.
	Список литературы

1. Определить глубину равномерного движения h_o1 и ширину канала по дну b на подводящем участке канала при β = (β _г.н.)_пред.

 Основная расчётная зависимость для каналов с равномерным движением воды это формула Шези:

                           ,                             (1)

где -площадь живого сечения

     -коэффициент Шези,

     -гидравлический радиус,

     - пьезометрический уклон дна.

  В данной задаче в число искомых величин входят   и , поэтому эта задача решается путём подбора. Определим необходимый модуль расхода по формуле:

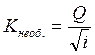                            ,                               (2)

  В нашем случае:

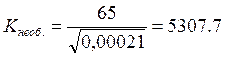                       м³/с,

  Определим относительную ширину канала по дну:

                      ,

                      ,

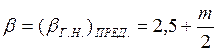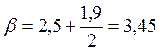  Будем задаваться глубиной потока и определять:

                      ,

  Результаты расчёта сведём в таблицу:

Таблица 1

Задаваемые и определяемые величины	Ед.изм	Численные значения			Примечания
h	м	4	3,8	3,6
b=b*h	м	13,8	13,1	12.42
w=(в+m*h)h	м2	85,6	77,25	69,34
c=в+h(2*Ö1+ m2)	м	30,98	29,43	27,88
R=w/c	м	2,76	2,63	2,49
C=(1/n)*R1/6	Öм/с2	49,36	48,94	48,49
K=w*C*ÖR	м3/с	7024,4	6126,3	5303,2

Проводим проверку:

Последний полученный результат удовлетворяет 5%-му расхождению с  и поэтому выбираем глубину равномерного движения , а ширину канала по дну на подводящем участке .

Пример расчета одной строки таблицы (для h = 4м):

а) ширина канала по дну ищется по формуле:

b=b∙h=3.45*4=13.8 (м),

б) площадь живого сечения ищем по формуле:

w=(b+m∙h)h=(13.8+1.9*4)∙4=85.6 (м);

в) смоченный периметр вычисляется по формуле:

c= b+ h(2∙Ö1+m²)=13.8+4∙(2∙Ö1+1.44)=30.98 (м);

г) гидравлический радиус определяется по формуле:

R=w/c=85.6/30.98=2.76 (м);

д) коэффициент Шези рассчитывается по следующей формуле:

C=(1/n)∙R^1/6=(1/0.024)∙ 2.76^1/6=49.36 (м/с²)^1/2.

где  n - коэффициент шероховатости;

е) модуль расхода ищется по формуле:

K=w∙C∙ÖR=85.6∙49.36∙Ö2.76=7024,4 (м³/с).

2. Определить глубину равномерного движения на отводящем участке канала , полагая ширину канала , равной найденной в п. 1.

    Для отводящего участка нам известно:

                  расход - Q=65 м³/с;

                  коэффициент откоса канала - m=1.9;

                  уклон для отводящего участка канала                   

                 i₂=      1.2∙i₁=1.2∙0.00015=0.00018;

                 коэффициент шероховатости - n=0.024;

         ширина канала по дну – b=12.42 м.

Для данного канала Kнеобх=Q/Öi2=65/Ö0.00018=4844.81(м³/с).

Далее составляем таблицу 2, в которой задаёмся рядом значений h, и для каждого h вычисляем соответствующий модуль расхода К.

Таблица 2

Задаваемые и определяемые величины	Ед.изм	Численные значения			Примечания
h	м	4	3.5	3.4
b	м	12.42	12.42	12.42
w=(в+m*h)h	м2	80,08	66.75	64.19
c=в+h(2*Ö1+ m2)	м	29.59	27.45	27.02
R=w/c	м	2.71	2.43	2.38
C=1/n*R1/6	Öм/с2	49.18	48.32	48.13
K=w*C*ÖR	м3/с	6479.7	5028.6	4761.8

Проводим проверку:

Последний полученный результат удовлетворяет 5%-му расхождению с  и поэтому выбираем глубину равномерного движения ,

В результате получаем h₀₂=3,4м при b=12,42м.

3. Определить средние скорости движения воды в канале и сравнить их с максимально допустимыми для заданного грунта скоростями

Значение средней скорости на данном участке при равномерном движении жидкости найдём из соотношения:

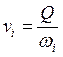                                   ,                                  (3.1)

отсюда    ,   .      

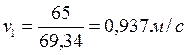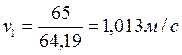Максимальные допустимые скорости воды для песка v=0.20-0.60 м/с, следовательно в канале будет происходить размыв русла. Для предотвращения размыва русла и образования наносов ниже по течению прибегают к его укреплению, например, наброской из камня.

4. При υ > υ_неразм определить глубину наполнения и уклон дна канала, полагая  υ = υ_неразм

  V_неразм определим по справочнику в зависимости от h и крупности частиц, слагающих русло канала.  В нашем случае V_неразм = 1,48 м/с.

Для расчета глубины канала воспользуемся следующим  соотношением:

,

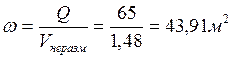которое получаем из формулы (3.1), затем подставляем в формулу: