Санкт-Петербургский государственный политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Расчётно-графическое задание №5
Дисциплина: Гидравлика
Тема: Расчет фильтрации воды через земляную плотину на водонепроницаемом основании
Выполнил студент группы № 3013/1 Широков Ю.А.
Преподаватель Локтионова Е.А.
“___”______________ 2012 г.
Санкт-Петербург
2012
Содержание
1)
Расчет
дамбы обвалования, расположенной на водопроницаемом основании и выполненной из
однородного изотропного грунта, имеющего коэффициент фильтрации ![]() такой
же, как и грунт водопроницаемого основания………………
такой
же, как и грунт водопроницаемого основания………………
a. Определение удельного фильтрационного расхода…………………………….
b. Построение кривой депрессии…………………………………………………..
c. Построение гидродинамической сетки …………………………………………
2) Расчет дамбы обвалования при наличии в ней трубчатого дренажа, перехватывающего расход воды, фильтрующейся через дамбу…………………...
a. Определение удельного фильтрационного расхода…………………………….
b. Построение кривой депрессии…………………………………………………...
c. Построение гидродинамической сетки …………………………………………
3) Список литературы....................................
1.
Расчет дамбы обвалования, расположенной на водопроницаемом основании и
выполненной из однородного изотропного грунта, имеющего коэффициент фильтрации ![]() такой же, как и грунт водопроницаемого
основания
такой же, как и грунт водопроницаемого
основания
a. Определение удельного фильтрационного расхода
Профиль плотины заменяется для расчета условным
профилем с вертикальным ограничением, доходящим до водоупора. Такое
вертикальное ограничение грунтового массива назначается на расстоянии ![]() от уреза воды в
верхнем бьефе (точка
от уреза воды в
верхнем бьефе (точка ![]() ), причем величина
), причем величина ![]() принимается
по формуле:
принимается
по формуле:

где ![]() - коэффициент откоса
верхнего бьефа.
- коэффициент откоса
верхнего бьефа.
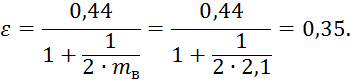
Значение величины ![]() равно:
равно:
![]()
В области низового клина условной плотины должно быть резкоизменяющиеся движение воды; в остальной же части условного тела плотины – плавно изменяющиеся движение.
Учитывая это обстоятельство, условная область
разбивается вертикалью на две части. Рассматривая далее два выделенных
фрагмента плотины в отдельности, и находятся удельные расходы ![]() для
каждого из них.
для
каждого из них.
1.
Первая
область плавно изменяющегося движения (I).
В этом случае для определения ![]() можно использовать
уравнение Дюпюи:
можно использовать
уравнение Дюпюи:
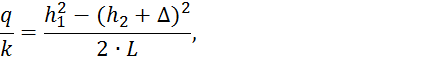
где
![]() - коэффициент
фильтрации, см/сек;
- коэффициент
фильтрации, см/сек; ![]() ,
, ![]() - глубины в верхнем и
нижнем бьефе соответственно, м;
- глубины в верхнем и
нижнем бьефе соответственно, м; ![]() - высота промежутка
высачивания, м;
- высота промежутка
высачивания, м; ![]() - горизонтальная
проекция с плавноизменяющимся движением, м.
- горизонтальная
проекция с плавноизменяющимся движением, м.
2.
Вторая
область резко изменяющегося движения (II
– низовой клин). Для определения величины ![]() в
случае низового клина плотины используется особый прием, который называется
приемом прямолинейных струек. По этому методу фильтрационный расход для II-ой
области определяется по формуле:
в
случае низового клина плотины используется особый прием, который называется
приемом прямолинейных струек. По этому методу фильтрационный расход для II-ой
области определяется по формуле:
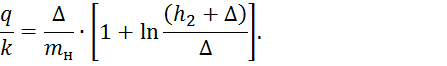
В результате
рассмотрения двух отдельных фрагментов, на которые был разбит условный профиль
дамбы, получилась система из двух уравнений с двумя неизвестными ![]() и
и
![]() :
:
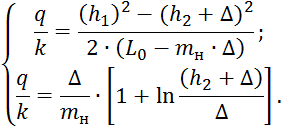
Эту систему уравнения
удобно решать графически: задаваться разными значениями ![]() и
вычислять величины
и
вычислять величины ![]() . Расчет представлен в
таблице 1.
. Расчет представлен в
таблице 1.
Таблица 1
|
|
|
|
|
|
м |
м |
м |
м |
|
1 |
29,84 |
2,174095 |
1,438464 |
|
2 |
28,04 |
2,121077 |
2,313117 |
|
3 |
26,24 |
2,022675 |
3,054849 |
|
4 |
24,44 |
1,868863 |
3,734596 |
|
5 |
22,64 |
1,646422 |
4,379482 |
|
6 |
20,84 |
1,337572 |
5,002584 |
Пример расчета для ![]() :
:
1. Горизонтальная проекция:
![]()
где все значения нам известны.
![]()
2. Отношение
![]() в области, где
плавноизменяющееся движение:
в области, где
плавноизменяющееся движение:
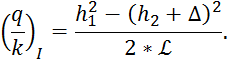
Подставив все значения в формулу, получаем:
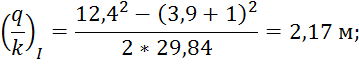
3. Отношение
![]() в области, где
резкоизменяющееся движение:
в области, где
резкоизменяющееся движение:
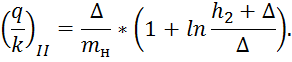
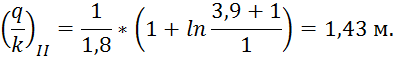
По полученным значениям строим 2
графика. Точка пересечения графиков и будет являться решением системы. Таким
образом, находим промежуток высачивания ![]() и величину (q/k)=2,1
м (рис. 2).
и величину (q/k)=2,1
м (рис. 2).
Зная величину ![]() , можно найти q:
, можно найти q:
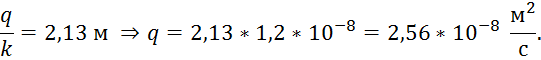
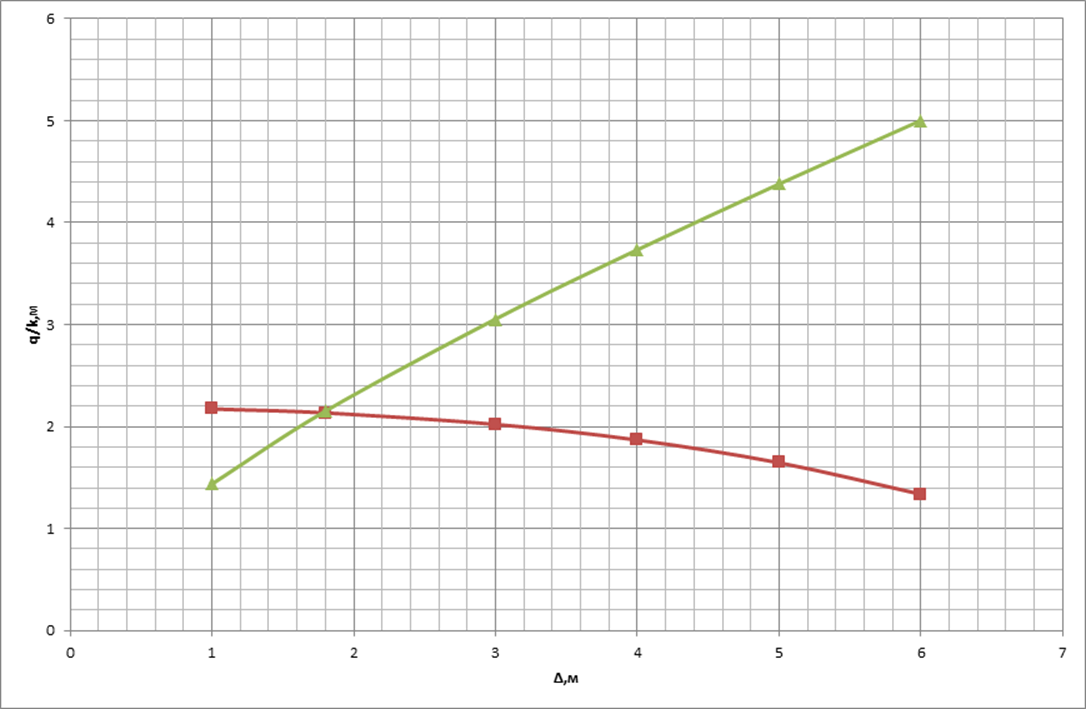
Рис. 1 Графики зависимостей (q/k)I=f(∆) и (q/k)II=f(∆).
1.2 Построение кривой депрессии
Кривая депрессии, для грунтовой дамбы, строится с помощью формулы Дюпюи:
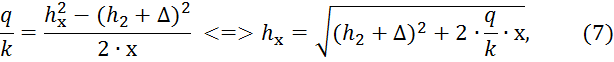
1.
где
![]() – расстояние,
отмеряемое от вертикальной оси, проходящей через точку пересечения низового
откоса дамбы и горизонтальной прямой, расположенной выше уровня воды в нижнем
бьефе на величину на промежуток высачивания.
– расстояние,
отмеряемое от вертикальной оси, проходящей через точку пересечения низового
откоса дамбы и горизонтальной прямой, расположенной выше уровня воды в нижнем
бьефе на величину на промежуток высачивания.
Длина расчетного участка ![]() равна:
равна:
![]()
Задавая расстояния ![]() (в пределах от 0 до
(в пределах от 0 до ![]() ) по формуле (7)
рассчитывается вертикальная координата кривой депрессии
) по формуле (7)
рассчитывается вертикальная координата кривой депрессии ![]() . Вычисления
представлены в таблице 2.
. Вычисления
представлены в таблице 2.
Таблица 2
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
28,4 |
||||||||||||
|
|
5,70 |
6,73 |
7,62 |
8,42 |
9,14 |
9,82 |
10,45 |
11,04 |
11,61 |
12,15 |
12,39 |
||||||||||||
Пример расчета для ![]() :
:
![]()
Получается, что отметка ![]() .
.
По данным таблицы 2 строится кривая депрессии (рис. 2).
Построенная кривая приходит в «расчетную» точку. Для того, что бы сделать
кривую депрессии соответствующей действительности, нужно соединить плавной
кривой точку ![]() и кривую депрессии
(см. рис. 2).
и кривую депрессии
(см. рис. 2).
1.3 Построение гидродинамической сетки
Гидродинамической сеткой называется система взаимно ортогональных линий тока и линий равного потенциала (напора).
Приведенный расход между кривой депрессии и
водоупором ![]() .
.
Разность напоров верхнего и нижнего бьефов равна:
![]()
Для построения гидродинамической сетки нужно разбить область фильтрации на целое число промежутков следующим образом:

где
![]() – целые числа.
– целые числа.
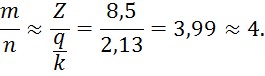
Допустим ![]() , тогда:
, тогда:
![]()
Гидродинамическая сетка построена на рис.3.
2. Расчет дамбы обвалования при наличии в ней дренажный банкет, перехватывающего расход воды, фильтрующейся через дамбу.
2.1 Определение удельного фильтрационного расхода
Поскольку нельзя допускать выхода промежутка
высачивания на низовой откос, нужно, чтобы кривая депрессии находилась под
поверхностью низового откоса на некотором расстоянии (не меньше, чем глубина
промерзания грунта ![]() ), чтобы зимой поток не
замерзал. Избежать этого можно, устроив в дамбе трубчатый дренаж,
перехватывающий расход воды, фильтрующейся через дамбу.
), чтобы зимой поток не
замерзал. Избежать этого можно, устроив в дамбе трубчатый дренаж,
перехватывающий расход воды, фильтрующейся через дамбу.
По аналогии с пунктом 1.1, действительный профиль
дамбы заменятся условным профилем с вертикальным ограничением, доходящим до
водоупора (рис.4). Такое вертикальное ограничение грунтового массива
назначается на расстоянии ![]() от уреза воды в
верхнем бьефе (точка
от уреза воды в
верхнем бьефе (точка ![]() ).
).
Фильтрационный расход можно определить
из формулы Дюпюи (при ![]() :
:

где ![]() - расстояние от
вертикального ограничения до трубчатого дренажа, м.
- расстояние от
вертикального ограничения до трубчатого дренажа, м.
Расстояние ![]() определяется из геометрии:
определяется из геометрии:
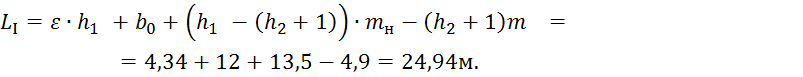
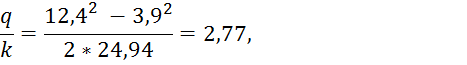
Удельный фильтрационный
расход ![]() равен:
равен:
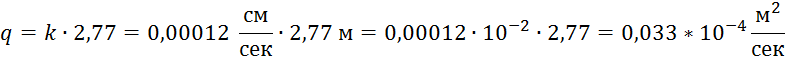
2.2 Построение кривой депрессии
Кривая депрессии, для
грунтовой дамбы, строится с помощью формулы Дюпюи (при ![]() ):
):
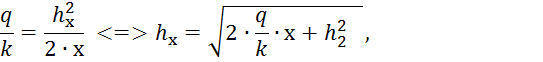
где ![]() - расстояние от
вертикальной оси, проходящей через дрену, до вертикального ограничения.
- расстояние от
вертикальной оси, проходящей через дрену, до вертикального ограничения.
Задавая расстояния ![]() (в пределах от 0 до
(в пределах от 0 до ![]() ) по формуле рассчитывается
вертикальная координата кривой депрессии
) по формуле рассчитывается
вертикальная координата кривой депрессии ![]() . Вычисления
представлены в таблице 4.
. Вычисления
представлены в таблице 4.
Таблица 4
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24,94 |
|
|
3,90 |
5,64 |
6,96 |
8,07 |
9,04 |
9,92 |
10,72 |
11,47 |
12,38 |
Пример расчета при ![]() :
:
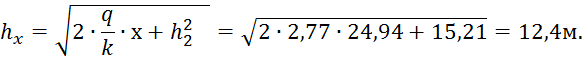
Получается, что отметка ![]() .
.
По данным таблицы 4 строится кривая депрессии (рис. 4).
Построенная кривая приходит в «расчетную» точку. Для того, что бы сделать
кривую депрессии соответствующей действительности, нужно соединить плавной
кривой точку ![]() и кривую депрессии
(см. рис. 4).
и кривую депрессии
(см. рис. 4).
2.3. Построение кривой депрессии и определение удельного фильтрационного расхода в предположении наличии ядра
Для построения кривой депрессии при наличия ядра используется виртуальная схема. Рассчитаем толщину виртуального ядра:
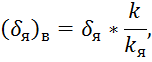
где
![]() - действительная
толщина ядра, м;
- действительная
толщина ядра, м; ![]() - коэффициент фильтрации
грунта тела ядра.
- коэффициент фильтрации
грунта тела ядра.
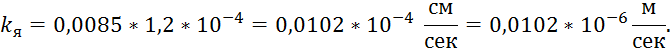
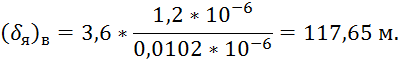
Далее найдем величину виртуальной горизонтальной проекции:
![]()
![]()
Найдем
отношение ![]() :
:
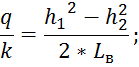
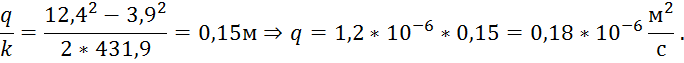
Для построения кривой депрессии воспользуемся уравнением:
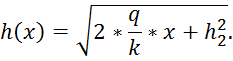
Для занесения результатов составим таблицу.
|
|
м |
0 |
3 |
6 |
9 |
12 |
12,8 |
436,3 |
438 |
440 |
444,84 |
|
|
м |
3,90 |
4,02 |
4,13 |
4,24 |
4,35 |
4,38 |
12,29 |
12,31 |
12,34 |
12,40 |
Пример расчета при ![]() :
:
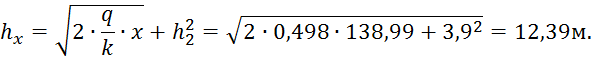
Получается, что отметка ![]() .
.
По полученным значениям строим кривую депрессии на виртуальной схеме (рис.6) и переносим ее на действительную (рис. 5).
2.4. Построение гидродинамической сетки при наличии ядра.
Гидродинамическую сетку строим таким образом, что линии равного гидродинамического напора и линии тока были друг другу перпендикулярны. По правую сторону от ядра единственная линия равного гидродинамического напора, она же кривая депрессии. Линии тока строим так, чтобы приблизительно получались квадраты.
По левую сторону от ядра у нас получилось две линии равного гидродинамического напора, которые приблизительно параллельные. Делим их на одинаковые участки и ведем под прямым углом к ним линии тока. Гидродинамическая сетка плотины представлена на рис.6.
Список литературы
1. Чугаев Р.Р. Гидравлика. Л.: Энергия, 1982. 672 с.
2. Гиргидов А.Д. Механика жидкости и газа (гидравлика). СПб.: Изд-во СПбГПУ, 2003. 544 с.
3. Механика жидкости и газа (гидравлика): методические рекомендации для выполнения и оформления курсовых и расчетно-графических работ / Сост.: Е.Н. Кожевникова, Е.А. Локтионова, В.Т. Орлов. СПб.: Изд-во Политехн. Ун-та, 2006. 39 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.