Гидравлический расчет элементов водохозяйственного комплекса

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Расчетно-графическое задание №4

Дисциплина: Гидравлика

Тема: Гидравлический расчет элементов водохозяйственного комплекса

Выполнил студент группы 3013/1             Шепетько В.В.

     Преподаватель                                         Локтионова Е.А.

«_____»______________2011г.

Санкт-Петербург

2011

Оглавление

1. Расчет каналов на равномерное движение………...……………………………4

 1.1. Определение нормальной глубины и ширины канала по дну на 

         подводящем участке канала……..………………………………………...….4

 1.2. Определение нормальной глубины на отводящем участке

         канала…………………………………………………………………………...6

 1.3. Определение средних скоростей движения воды в каналах
         и сравнения их с допустимыми…………………………………………..…...8

 1.4. Определение глубины наполнения и уклона дна на
         подводящем участке канала…………………………………………………10

 1.5. Определение критической глубины и критического уклона………………11

 1.6. Построение графика удельной энергии сечения……………………………15

2. Расчет каналов на неравномерное движение….……………………………….19
  2.1. Построение кривой свободной поверхности на подводящем
         участке канала………………………………...………………………………19

  2.2. Построение кривых свободной поверхности на отводящем
         участке канала………………………………………………………………...23

3. Расчет гидравлического прыжка………………………………………………..30

  3.1. Построение графика прыжковой функции……………….………………...30

  3.2. Определение местоположения гидравлического прыжка…………………32

  3.3. Определение параметров гидравлического прыжка……………………….34

Литература…………………………………………………………………………..36

1. Расчет каналов на равномерное движение

1.1. Определение нормальной глубины и ширины канала по дну на подводящем участке канала

В данном пункте необходимо определить нормальную глубину (h_o1) и ширину канала по дну (b). Воспользуемся формулой Шези:

 ,

   где Q – установившейся поток, м³/с,

         ω – площадь живого сечения, м²,

          C – коэффициент Шези,  ,

          R – гидравлический радиус, м,

          i₁ – продольный уклон дна.

Площадь живого сечения исходя из геометрических соображений можно найти по следующей формуле:

 ,

   где m – заложение откоса канала (коэффициент бокового откоса).

Коэффициент Шези находится по формуле Маннинга:

 ,

   где n – коэффициент шероховатости.

Гидравлический радиус по определению есть отношение площади живого сечения к смоченному периметру (χ, м):

 .

Смоченный периметр вычисляется по следующей формуле:

 .

Рассчитаем необходимый модуль расхода K_{необх 1} :

 ,

 .

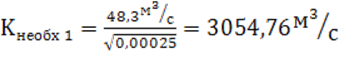Рассчитаем относительную ширину канала, которая соответствует гидравлически наивыгоднейшему сечению:

 ,

 .

Решение всех выше перечисленных уравнений в данном случае лучше путем подбора. Составим таблицу (табл.1), в которой в зависимости от нормальной глубины канала мы получаем такой модуль расхода, чтобы он был близок к необходимому модулю расхода.

Таблица 1. Подбор нормальной глубины канала

ho1	м	1	2	2,5	2,8	3
b = β*ho	м	3,45	6,9	8,625	9,66	10,35
ω	м2	5,35	21,4	33,44	41,944	48,15
χ	м	7,74	15,49	19,36	21,68	23,23
R	м	0,69	1,38	1,73	1,93	2,07
C		55,3	62,07	64,45	65,64	66,41
		245,76	1560,4	2834,73	3824,87	4600,61

Пример расчета таблицы 1 для h_o1=1м:

1) h_o1=1м ;

2) b = 3,45*1м = 3,45м ;

3) ω = (3,45м + 1,9*1м)*1м = 5,35м² ;

4) χ = ;

5)  ;

6)  ;

7) К = 5,35м² * 55,3 * = 245,76  .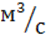

Построим график зависимости нормальной глубины на подводящем участке канала от модуля расхода (рис.1). Из графика видно, что при
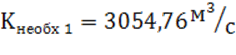  нормальная глубина составляет h_o1 = 2,57м. Тогда ширина канала по дну будет b = (β_г.н.)_пред*h_o1 = 3,45*2,57м =  8,67м.

1.2. Определение нормальной глубины на отводящем участке канала

В данном пункте необходимо определить нормальную глубину на отводящем участке канала (h_o2) при ширине канала по дну b = 8,67м (найдено в п. 1.1). Для этого воспользуемся теми же формулами, что и в пункте 1.1 и получим следующую таблицу значений:

Таблица 2. Подбор нормальной глубины канала

ho2	м	1	2	2,5	2,8	3
ω	м2	10,57	24,94	33,55	39,172	43,11
χ	м	12,96	17,26	19,41	20,69	21,55
R	м	0,82	1,45	1,73	1,89	2,0005
C		56,91	62,58	64,45	65,41	66,03
		544,72	1879,37	2844,1	3522,5	4026,14

Пример расчета таблицы 2 для h_o1=1м:

1) h_o1=1м ;

2) b = 8,67м ;

3) ω = (8,67м + 1,9*1м)*1м = 10,57м² ;

4) χ = ;

5)  ;

6)  ;

7) К = 10,57м² * 56,91 * = 544,72  .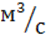

Рассчитаем необходимый модуль расхода K_{необх 2} :

 ,

 .

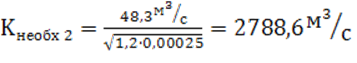Построим график зависимости нормальной глубины на отводящем участке канала от модуля расхода (рис.2). Из графика видно, что при
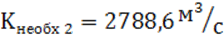  нормальная глубина составляет h_o2 = 2,47м.

1.3. Определение средних скоростей движения воды в каналах и сравнения их с допустимыми

В данном пункте необходимо найти средние скорости движения воды на подводящем и отводящем участках канала. Поток воды на этих участках одинаков (Q=const), различаются только площади живого сечения. По определению средняя скорость находится по формуле:

 .

Соответственно, средняя скорость движения воды на подводящем участке канала:

 ,           ,

 ,

 .

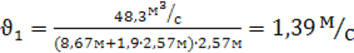На отводящем участке канала:

 ,           ,

 ,

 .

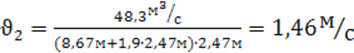Теперь найдем допускаемые скорости движения воды в каналах. Так как глубины каналов разные, то соответственно будут две разные допустимые скорости. Определить эти скорости можно воспользовавшись [1] (табл.7.1, стр.72).

Допустимая скорость – это функция, зависящая от диаметра частиц песка, слагающего русло канала (d) и от глубины канала (h_o):

 ,

d = 2мм,   h_o1 = 2,57м   →   υ_{доп 1} = 0,77м/с ,

  d = 2мм,   h_o2 = 2,47м   →   υ_{доп 2} = 0,766м/с .

1.4.Определение глубины наполнения и уклона дна на подводящем участке канала

Данный пункт выполняется при υ₁ > υ_{доп 1} . В данном случае υ₁ = 1,39м/с больше, чем υ_{доп 1} = 0,77м/с . Допустим, что υ₁ = υ_{доп 1} и найдем глубину наполнения и уклона дна канала.

 ,

 .

Приравняем эти два уравнения и получаем следующее:

    ,

    ,

    ,

   D = b² – 4ac = (8,67)² + 4*1,9*62,73 = 551,92 ,

    .

Чтобы определить уклон дна, воспользуемся формулой Шези:

    →     ,

 ,

 ,

 ,

 ,

 ,

 ,

,

 ,

 .

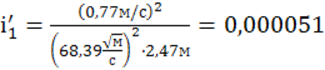Изобразим как выглядят наши каналы при различных глубинах. Схемы представлены на рис.3.

1.5. Определение критической глубины и критического уклона