Определение средний скорости движения, глубину равномерного движения воды в канале. Определение критической глубины и критического уклона в канале, страница 2

Подставляем числа и решаем квадратное уравнение:

;

,

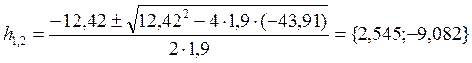выбираем 2,545 , т.к. второе решение меньше нуля. Определим значения величин, которые понадобятся в дальнейшем:

Таблица 2

Задаваемые и определяемые величины	Ед.изм	Численные значения
h	м		2,545
b	м		12,42
w	м2		43,99
c	м		23,38
R	м		1,88
C	Öм/с2		46,29
K	м3/с		788,55

Уклон дна получим из формулы Шези:       

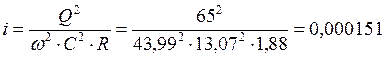
5. Определить критическую глубину h_к и критический уклон i_к

Критической глубиной называется  глубина, соответствующая минимуму удельной энергии поперечного сечения. Исходя из этого,   найдем данную величину из выражения для производной функции удельной энергии сечения, приравненного к нулю:

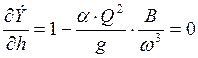,                          (5.1)

где  = 1 – корректив кинетической энергии; Q = 65 м³/с – расход воды в канале; g = 9.8 м/с² – ускорение свободного падения; -  площадь живого сечения канала; B – ширина потока (канала) поверху.

Из формулы получаем следующее выражение:

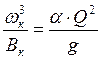,                              (5.2)

где: ,  - площадь живого сечения и ширина потока поверху соответственно, при h = h_к.

Решать такое уравнение будем методом подбора. Для этого сначала вычислим значение выражения:

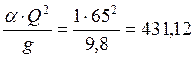м⁵ ,

затем при различных значениях h подсчитаем значение величины . Результаты сведем в таблицу 4:

Таблица 4.

Пример расчета:  тогда

    

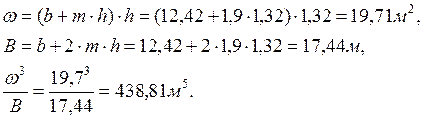
  Относительная погрешность составляет менее 2%, и окончательно  принимаем значение критической глубины h_к = 1.32м.

  Критическим уклоном называют воображаемый уклон, который надо придать рассматриваемому призматическому руслу, что бы при заданной величине расхода и равномерном движении, нормальная глубина оказалась равной критической. Для определения этой величины воспользуемся  формулой:

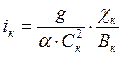     ,                              (5.3)

     здесь индекс «к» означает значение величин, вычисленных при критической глубине h_к  = 1.32 м, а именно:

                  b = 12.42 м; B_к = 17.44 м; _к = 19.7 м².

Остальные величины определим по формулам п.1:

    ;

    ;

   

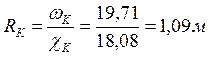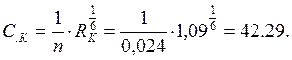
Тогда по формуле (5.3):

    .

6. Построение графика удельной энергии сечения Э = f (h).

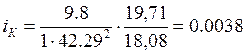       Для нахождения значений удельной энергии сечения воспользуемся следующим уравнением:

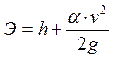                                 (6.1)

где:  = 1 – корректив кинетической энергии; g = 9.8 м/с² – ускорение свободного падения;  - площадь живого сечения;

v – средняя скорость (v = Q/).

Для построения графика составим табл. 5.

Таблица 5.

h, м	b, м	, м2	v, м/с	Э, м
0,5	12,42	6,69	9,72	5,32
0,75	12,42	10,38	6,26	2,75
1	12,42	14,32	4,54	2,05
1,25	12,42	18,49	3,51	1,88
1,5	12,42	22,91	2,84	1,91
1,75	12,42	27,55	2,36	2,03
2	12,42	32,44	2,00	2,20
2,25	12,42	37,56	1,73	2,40
2,5	12,42	42,93	1,51	2,62
2,75	12,42	48,52	1,34	2,84
3	12,42	54,36	1,20	3,07
3,25	12,42	60,43	1,08	3,31

Пример расчета:

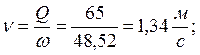
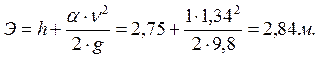
По найденным значениям Э строим график Э = f (h) (см. рис. 3).

7. Построение  кривой свободной поверхности на подводящем участке канала (от 1,05*h₀₁ до h_р).

  Тип кривой свободной поверхности будет а₁, так как i < i_k  и h₀₁<h_p.         Она строится методом Чарномского на основании вычислений, выполненных в таблице 6, при этом будут рассматриваться глубины:

     h_p - глубина воды в канале перед регулирующим сооружением:

м.

     h_нач - глубина в начале рассматриваемого участка канала:

м.

Для построения зададимся шаго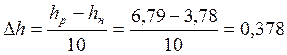м:

м.

Для вычисления необходимых величин используются  вышеприведенные формулы. Значение Э считается по формуле (6.1). Величину среднего уклона трения и длину участка находим по формулам:

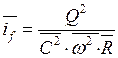                                                ;                                                 (7.1)

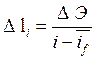,                                                      (7.2)

где:  i = 0.0005 - уклон дна на подводящем участке канала (найденный в п. 4).

Таблица 6.

№	H,м	Э, м	∆Э, м			, м
1	3,78	3,81	0,368	0,0001045	0,0000465	7852
	4,08	4,10
2	4,08	4,10	0,371	0,0000737	0,0000773	4771
	4,38	4,40
3	4,38	4,40	0,372	0,0000533	0,0000977	3797
	4,68	4,70
4	4,68	4,70	0,374	0,0000394	0,0001116	3337
	4,98	5,00
5	4,98	5,00	0,374	0,0000297	0,0001213	3077
	5,29	5,30
6	5,29	5,30	0,375	0,0000227	0,0001283	2916
	5,59	5,60
7	5,59	5,60	0,376	0,0000177	0,0001333	2809
	5,89	5,90
8	5,89	5,90	0,376	0,0000139	0,0001371	2735
	6,19	6,20
9	6,19	6,20	0,376	0,0000111	0,0001399	2681
	6,49	6,50
10	6,49	6,50	0,376	0,0000089	0,0001421	2642
	6,79	6,80
						36617,90

Пример расчета:

,

.

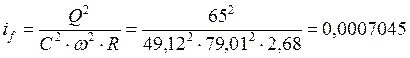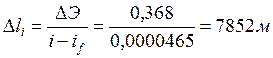По данным табл. 6 строим кривую свободной поверхности типа a1 на подводящем участке канала вверх по течению, т.е. начинаем с конца табл.6. (см. рис. 4).

8. Построить кривые свободной поверхности на отводящем участке канала при условиях: а) открытие затвора е=0,3h_к б) глубина воды в конце канала равна h_k

 На отводящем участке будет две кривых свободной поверхности с₁ и b₁. Сначала построим первую из них.

 А) Глубина  считается по формуле:

,                               (8.1)

  где м - критическая глубина (п.5);

                        м. 

  Глубина  равна: