Определение средний скорости движения, глубину равномерного движения воды в канале. Определение критической глубины и критического уклона в канале, страница 3

        м.                      (8.2)

  Поступая аналогично п.7. найдем  шаг  по глубине:

.     

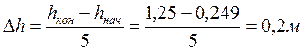                                                                                     Таблица 7.

№	H,м	Э, м	∆Э, м			, м
1	0,25	21,16	14,673	0,513457	0,513306	28,6
	0,45	6,49
2	0,45	6,49	3,112	0,111170	0,111019	28,0
	0,65	3,38
3	0,65	3,38	1,019	0,038707	0,038556	26,4
	0,85	2,36
4	0,85	2,36	0,371	0,017233	0,017082	21,7
	1,05	1,99
5	1,05	1,99	0,108	0,008920	0,008769	12,3
	1,25	1,88
						117,1

На этом участке движение бурное, строим кривую с₁ вниз по течению (см. рис.5).

Б) Для построения кривой b₁ определим длину отводящего участка канала:

                                м.

Глубину в начале определим по формуле:

                      ,                                 (8.3)

где  возьмем из п.2.:

                                  м.

Глубину в конце участка примем равной:

                          м.

Составим табл. 8. (аналогично табл.7.):

                                                                                                 Таблица 8.

№	H,м	Э, м	∆Э, м			, м
1	3,23	3,29	0,347	0,0002811	0,0001301	2676,6
	2,86	2,94
2	2,86	2,94	0,334	0,0004531	0,0003021	1108,5
	2,49	2,61
3	2,49	2,61	0,311	0,0007785	0,0006275	495,8
	2,12	2,30
4	2,12	2,30	0,263	0,0014576	0,0013066	201,6
	1,75	2,03
5	1,75	2,03	0,154	0,0030856	0,0029346	52,4
	1,38	1,88
						4534,9

По данным таблицы строим кривую типа b₁, см. рис.5.

9. Построить кривую свободной поверхности на подводящем и отводящем участках канала при полностью открытом затворе

     На отводящем участке канала будет кривая типа b₁, построенная в п.8., для построения кривой на подводящем участке поступим аналогично п.8., составляя таблицу 9, при этом примем:

м.

3.23м (из пункта 8, определенную по графику):

                                                                                       Таблица 8.

№	H,м	Э, м	∆Э, м			, м
1	3,42	3,47	0,0364	0,0001861	0,0000351	1048,8
	3,38	3,44
2	3,38	3,44	0,0364	0,0001941	0,0000431	850,8
	3,34	3,40
3	3,34	3,40	0,0363	0,0002026	0,0000515	709,2
	3,31	3,36
4	3,31	3,36	0,0362	0,0002115	0,0000604	602,9
	3,27	3,33
5	3,27	3,33	0,0362	0,0002208	0,0000698	520,4
	3,23	3,29
						3732

На подводящем участке канала будет кривая типа b₁ (см.рис.6).

10. Построить график прыжковой функции θ(h), совместив его с графиком удельной энергии сечения Э(h)

Составим табл.10, в которой зададимся рядом значений h и для каждого h вычислим прыжковую функцию. При этом помимо ранее использовавшихся, будем применять следующие формулы:

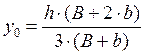 ,                                 (9.1)

где  - заглубление под уровнем жидкости центра тяжести.

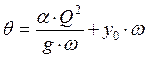.                                 (9.2)

Таблица 10.

	h,м		y0,м
1	0,5	6,69	0,24	66,12
2	1	14,32	0,48	36,95
3	1,2	17,64	0,57	34,48
4	1,4	21,11	0,66	34,33
5	1,6	24,74	0,75	35,92
6	1,8	28,51	0,84	38,93
7	1,9	30,46	0,88	40,92
8	1,95	31,44	0,90	42,02
9	2	32,44	0,92	43,20
10	2,5	42,93	1,13	58,75
11	3	54,36	1,34	80,92

Пример расчета:

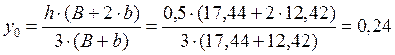м,

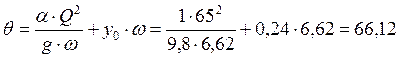м³.

График представлен на Рис.3.

11. Построить линию сопряженных глубин для кривой типа c₁ и определить местоположение прыжка.

Глубины кривой типа c₁ найденные в п. 8 используем в качестве первых сопряженных глубин h` при построение линии сопряженных глубин для кривой типа c₁.

По графику прыжковой функции находим вторые сопряженные глубины h`` (рис.3):

Таблица 11.

Получившиеся вторые сопряженные глубины наносим на рис. 4. Продлевая до точки пересечения со свободной поверхностью, находим вторую сопряженную глубину (h`` = 3.2м). По графику прыжковой функции находим первую сопряженную глубину (h` = 0.85м), тем самым, определяя местоположение прыжка.

12. Определить длину гидравлического прыжка и потери энергии в нем. Представить на рисунке схему гидравлического прыжка и показать на ней напорную линию.

Найдем:

а) высоту прыжка:

;                                  (12.1)

                         м.

б) длину гидравлического прыжка:

м;

м;

м.

в) площадь поперечного сечения канала в начале и конце гидравлического прыжка:

м;

м.

г) средние скорости течения воды в начале и в конце прыжка:

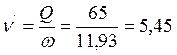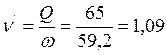м/с;

м/с.

д) скоростной напор в начале и в конце прыжка:

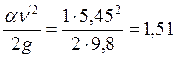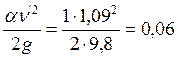м;

м.

Пьезометрическая линия проходит по уровню свободной поверхности воды, а напорная линия отличается от нее на величину скоростного напора (рис. 7).

Потери энергии в гидравлическом прыжке считаем по формуле:

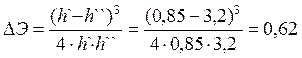м

 

3. Список литературы

       1. Чугаев Р.Р.  Гидравлика ( техническая механика жидкости ). - Л.: Энергоиздат, 1982. - 672 с.

       2. Кожевникова Е.Н., Орлов В.Т. Методические указания по выполнению курсовых и расчетно-графических работ по курсу гидравлики. - Л. : Издание ЛПИ им. М.И. Калинина, 1985. - 48 с.

       3. А.Д. Гиргидов. «Техническая механика жидкости и газа» - Спб, издательство СПбГТУ, 1999г.