Дедуктивное рассуждение отличается от индуктивного достоверностью заключения, т.е. в дедуктивном рассуждении заключение истинно, по крайней мере, когда истинны все посылки. В отличии от неполной индукции и аналогии в дедуктивном рассуждении нельзя получить ложное суждение из истинных посылок.
Широкое применение дедукции в математике обусловлено аксиоматическим методом построения теории, заключающейся в том что часть утверждений принимается за истинные без доказательства (аксиомы), истинность остальных доказывается логическим путем из аксиом.
Как метод исследования дедукция характеризуется тем, что для получения знания о новом объекте, находят класс объектов, ближайших к исследуемому, и свойства этого класса переносят на исследуемый объект.
Изучая свойства квадрата, мы сначала устанавливаем, что квадрат является ромбом и все свойства ромба приписываем квадрату.
В процессе изучения математики индукция и дедукция не выступают изолированно, а тесно взаимосвязаны.
«Индукция и дедукция связаны между собой столь же необходимым образом, как синтез и анализ. Вместо того, чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться применять каждую на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг друга»
Ф. Энгельс
Приступая к изучению теоремы Виета, можно индуктивно подвести учащихся к закономерности для корней квадратного уравнения, затем дедуктивно доказать их свойства. (Лаб. Работа о свойствах средней линии треугольника и трапеции подводят учащихся к формулировке теорем, доказательство осуществляется дедуктивным методом).
Особенно тесно связь индукции и дедукции проявляется в методе совершенной индукции, состоящей из последовательных этапов:
1. наблюдение и опыт;
2. гипотеза;
3. доказательство гипотезы.
1. Вычислить сумму: 
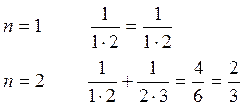
2. Гипотеза: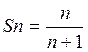 
3. Доказательство гипотезы осуществим
методом математической индукции а)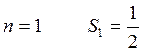 
истина б) докажем, что из истинности 
следует истинность 
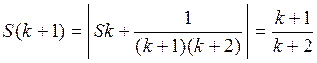
в) по аксиоме индукции 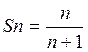для 
8. Метод математической индукции.
Метод математической индукции основан на аксиоме математической индукции:
«Если некоторое утверждение, сформулированное для натурального числа n, истинно для n = 1 и из допущения истинности его для произвольного числа n = k следует истинность его для n = k + 1 (следующего за числом k), то это утверждение истинно для любого натурального числа n.»
Символически это выражается формулой:
базис индукционный индукции шаг
Метод этот непривычен и труден для учащихся, поэтому необходимо изложить и объяснить его обстоятельно закрепить его основательно на различных примерах.
Иногда индукционное предложение P(h) не имеет смысла для некоторых первых натуральных чисел, тогда принцип математической индукции формулируется так:
Наибольшую трудность в
реализации этого метода вызывает второй шаг, где приходится доказывать
истинность импликации 
.
Для овладения методом математической индукции полезно решить с учащимися примеры следующих типов:
1. Доказать формулу суммы n членов арифметической и геометрической прогрессий.
2. Доказать делимость 
на 27; 
на 9
3. Доказать неравенство 
при 
4. Доказать, что плоскостей, из которых
никакие две не параллельны и никакие три не проходят через одну точку, делят
пространство на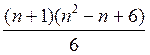 
частей.
Литература
1. Методика преподавания математики / Сост. А.Я. Блох, Р.С. Черкасов. – М: Просвещение, 1985, 336с.
2. Ю.М. Колягин и др. Методика преподавания математики. – М: Просвещение, 1975, - 462с.
3. П.М. Эрдниев. Преподавание математики в школе. – М: Просвещение, 1978. – 304с. (Обобщ. и анализ. стр. 74, анализ и синтез – стр. 103, связь индукции и дедукции стр. 88)
4. П.М. Эрдниев. Сравнение и обобщение при обучении математике. –М: Учпедгиз, 1960. – 150с.
5. А.Я. Цукарь. Использование аналогий в преподавании математике. /ж. «Математика в школе № 4 – 1981г. стр. 22
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.