Электрореактивная двигательная установка на базе ПИД для коррекции орбиты космического аппарата, страница 15

Все величины, входящие в числитель формулы (1,43), известны:

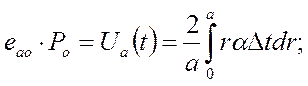                            (1.44)

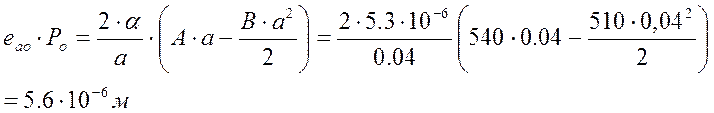
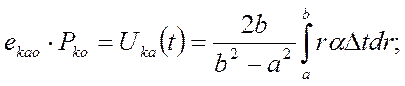                           (1.45)

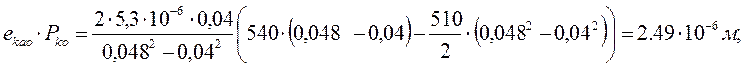
Податливости еа, ека, входящие в знаменатель формулы (5.3), найдем из рисунка 1,8.

Если приложить распределенное усилие R к радиусу а электрода, то податливостью последнего будет называться отношение:

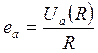;                                                    (1.46)

Удлинение электрода на радиусе а от нагрузки R:

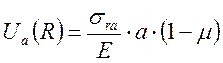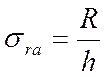, ;                               (1.47)

Откуда 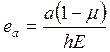                                    ;                                                  (1.48)

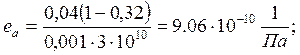
Аналогично, податливость кольца :

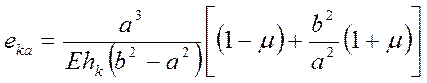                            (1.49)

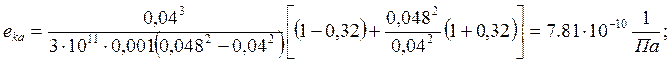
Следовательно, из формулы (1.47) найдем R:

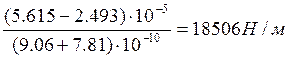
Напряжения для сетки определяются по формулам:

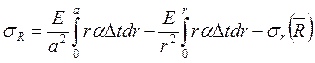;                         (1.50)

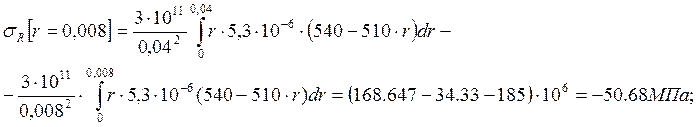
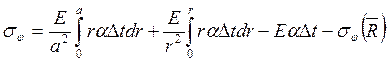;                       (1.51)

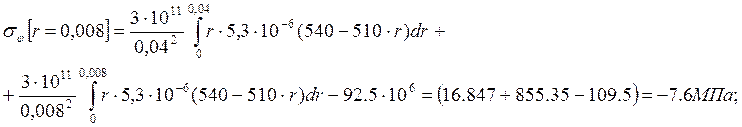
где 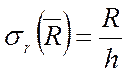   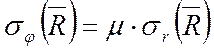            ,                ;             (1.52)

или сокращенно:

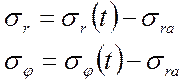                                      (1.53)

где  - температурные составляющие напряжений в формуле (1.53), где                                            .

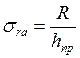Так как пластина перфорированная, то hпр=h, где  - коэффициент перфорации пластины.

Значение коэффициента рассчитывается по формуле:

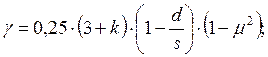                                  (1.54)

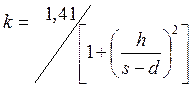                                               (1.55)

Обычно [1]

Напряжения в кольце найдем по формулам:

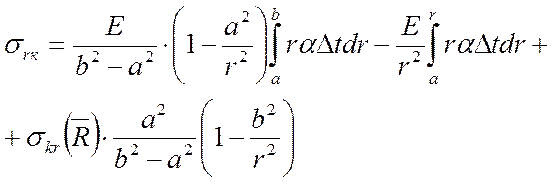;(1.56)

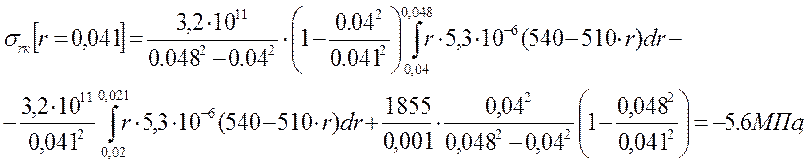
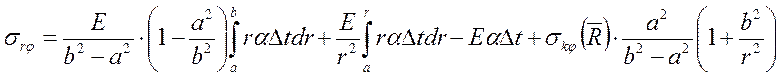
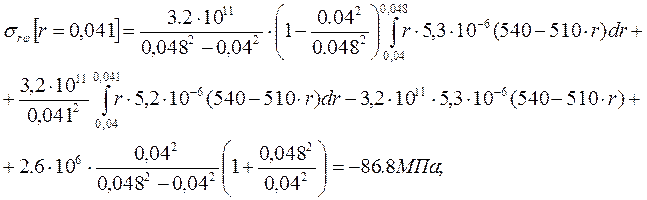;              (1.57)

или сокращенно : 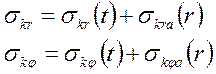                                          (1.58)

где  - температурные составляющие напряжений;

 .

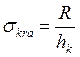Эквивалентное напряжение в наиболее нагруженной точке (r = 0) можно определить по следующей формуле:

                                    (1.59)

Для сетки:           

Для кольца:                   

Расчет заканчиваем проверкой запаса прочности по формуле:

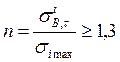                                                           (1.60)

Для сетки:

=240 МПа при t=550К, [1].

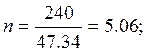
Для кольца:

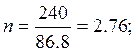
В результате расчетов проверили запас прочности электродов, он получился больше заданного. Следовательно, рассчитанный элемент конструкции должен работать при заданных параметрах на протяжении всего срока своей эксплуатации.

1.10.2 Расчет физической надежности ускоряющего электрода ИОС

Ускоряющий электрод ИОС изготовлен из молибдена

Для определения физической надежности ускоряющего электрода ИОС воспользовались следующей формулой:

,

(1,61)

где -предел длительной прочности материала ускоряющего электрода ИОС  МПа;

-эквивалентное напряжение в наиболее нагруженной точке,  МПа;

-среднеквадратичное отклонение эквивалентного напряжения в наиболее нагруженной точке:

МПа

(1.62)

Необходимо определить среднеквадратичного отклонения эквивалентного напряжения в наиболее нагруженной точке для этого найдем факторы от которых оно зависит.

Зависит оно от следующих факторов:

 – расстояние между отверстиями;        

 – диаметр отверстий;                          

 – толщина электрода;                            

 – толщина кольца;                                

 – радиус кольца;                                     

 – радиус электрода.                               

Тогда выражение для определения среднеквадратичного отклонения эквивалентного напряжения в наиболее нагруженной точке можнонайти по формуле:

,

(1.63)

где,  -среднеквадратичное отклонение расстояния между электродами ИОС, мм;

-среднеквадратичное отклонение диаметра отверстий ускоряющего электрода ИОС, мм;

-среднеквадратичное отклонение толщины ускоряющего электрода ИОС, мм;

-среднеквадратичное отклонение толщины кольца, мм;

-среднеквадратичное отклонение внешнего радиуса кольца  мм;

-среднеквадратичное отклонение радиуса ускоряющего электрода ИОС, мм;

Используя программу, написанную в MathCAD (Приложение 2) определим частные производние от эквивалентного напряжения по соответствующим факторам: