Электрореактивная двигательная установка на базе ПИД для коррекции орбиты космического аппарата, страница 14

FF – значение магнитного потока, Тлм²

L – длина ионизационной камеры, м

L_c – координата катодного блока, отсчитана от анода, м

L_p – ширина полюсного наконечника, м

Результаты расчета приведены в таблице 1.4.

Табл. 1.4

Id, А	Ud, В	Ci, В	Bo, Тл	FF, Тлм2	L, м	Lc, м	Lp, м
1.233	96.4667	277.9195	0.04110	1.2101*10-3	0.08174	0.04087	0.04087

На рис 1.3 приведены характерные размеры, полученные в результате расчета программы

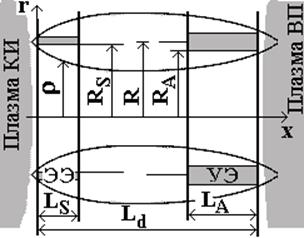
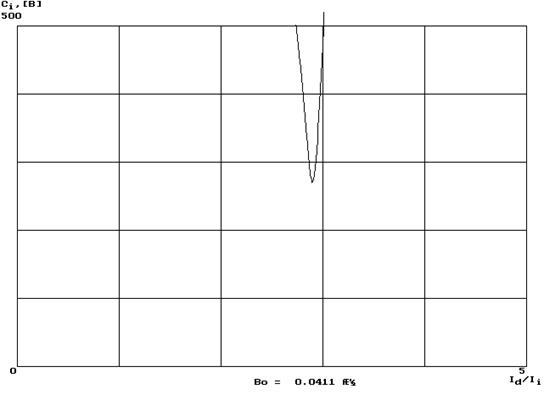Рис.1.4 график зависимости  к  с оптимальным значением магнитной индукции.

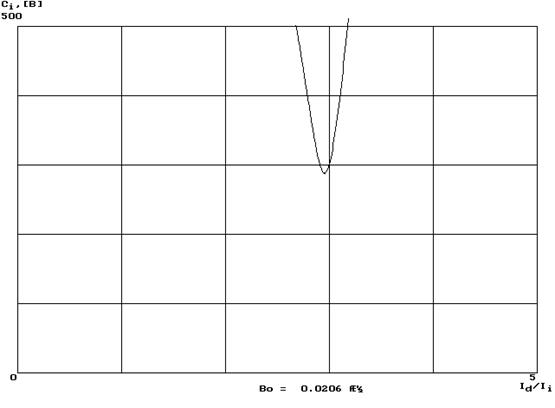
Рис.1.5 график зависимости  к  с минимальным значением магнитной индукции.

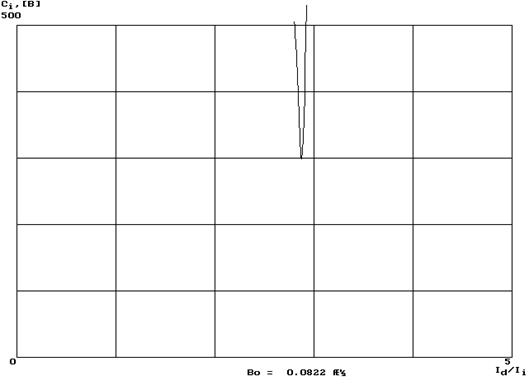
Рис.1.6 график зависимости  к  с максимальным значением магнитной индукции.

Ионно-оптическая система является одним из основных узлов, определяющих работу плазменно-ионного движителя. Точные расчеты, проектирование и изготовление ее электродов увеличивает тяговый КПД движителя и его ресурс.

1.10 Расчет на прочность и физическую надежность ускоряющего электрода ИОС

1.10.1 Расчет температурных напряжений в электродах ИОС.

Смыслом расчета на прочность движителя является нахождение запаса прочности деталей, которые работают длительное время в условиях высоких температур, температурных градиентов. В данной работе производится расчет на прочность ускоряющего электрода ионно-оптической системы ПИД, который заключается в определении температурных напряжений.

ИОС ПИД работает в тяжелых условиях, так как подвергается высоким температурным нагрузкам. В зависимости от ее прочностных характеристик зависит ресурс и к.п.д. движителя.  Вот поэтому очень важным является расчет электродов ИОС на прочность.

Электроды ИОС ПИД рассчитываются на основе расчета для  тонких электродов. Расчетная схема электрода ИОС ПИД  представлена на рис (1.6)

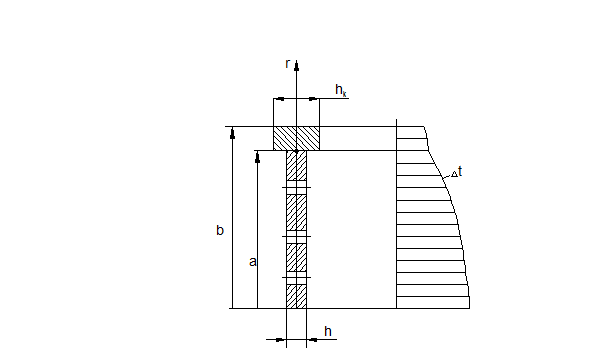
Рисунок 1.6. Расчетная схема электрода

Исходные данные для расчёта:

а) коэффициент линейного расширения материала экранного электрода (электрод изготовлен из материала Мо, ;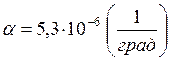

б) модуль упругости, ;

в) коэффициент Пуассона, ;

г) градиент температур по длине сетки,

;

А=540 К;

В=510К/м;

д) градиент температур по длине кольца,

Задаемся значениями температуры в трех точках по радиусу сетки, строим график градиента температур (рис.5.2), который используем в дальнейших расчетах.

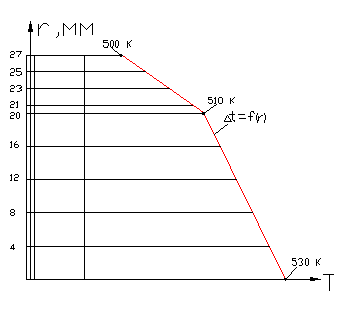ж) радиус сетки, а=40мм з)радиус кольца, b=48 мм;

и) толщина сетки, h=1 мм;

к) толщина кольца, h_k=1 мм.

При расчетах представляем, что электрод состоит из перфорированной пластины, являющейся собственно электродом, и силового кольца, которым электрод крепится к движителю. На рисунке 1.7 показана эпюра температур электрода при установившейся работе движителя. Неравномерный нагрев электрода вызывает температурные напряжения. Как видно из рисунка, температура средней части электрода выше чем периферийной, что может привести к выпучиванию электрода.

Итак, известны h, h_k , t, E, . Требуется найти , , U.

На стыке электрода и его силового кольца возникнут силы реакции R, которые следует определить.

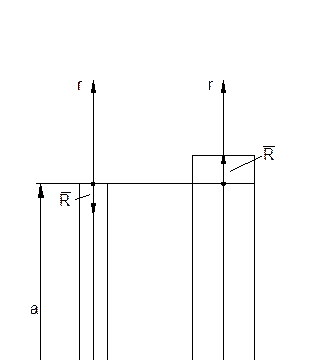Находим значение реакции R с помощью метода сил [1]. Для этого рассекаем кольцо и электрод по радиусу а, затем прикладываем неизвестную силу взаимодействия R (см. рис.5.3).Находим значение этой силы из условия равенства радиальных деформаций кольца Uka и электрода Ua на радиусе а:

                                 (1.41)

                          (1.42)

где ека , еа – податливость электрода и кольца в точке А от распределенной контурной нагрузки;

еа_о, ека₀ – податливость электрода и кольца от внешней нагрузки;

Р₀, Рк₀ – внешняя нагрузка на электрод и кольцо.

Учитывая, формулы (5.1), (5.2), получим выражение для R:

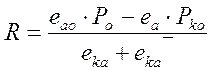;                                          (1.43)