Проектирование ядерной энергетической установки с многорежимными плазменными термоэмиссионными преобразователями: Учебное пособие, страница 5

На первом этапе производится расчет стационарных тепловых и электрических полей ЭГК и распределение температуры теплоносителя в активной зоне и холодильнике-излучателе, соответствующих начальному уровню тепловой мощности реактора (q_v(0,r,z)=q_v⁽⁰⁾(r,z)) и некоторому значению полного тока I⁽⁰⁾ в цепи ЭГК. Затем на каждом шаге по времени с учетом изменения объемной плотности тепловыделения по заданному закону q_v(t r,z) производится теплофизический расчет ЭГК и холодильника-излучателя, а также определение электрических характеристик ЭГК и всего реактора-преобразователя. На рис. 4 показана блок-схема алгоритма расчета.

Для численного решения двумерного нестационарного уравнения теплопроводности в ядерном сердечнике (1) используется метод переменных направлений. На каждом шаге по времени расчет температурного поля сердечника проводится методом прогонки. Данный метод отличается от других вариантов метода исключения неизвестных тем, что увеличение числа шагов не приводит к возрастанию погрешности решения.

Одномерные нестационарные уравнения (2…7) теплопроводности вдоль катодной оболочки, коммутационной перемычки и анода, а также уравнение теплопроводности для теплоносителя в активной зоне (9), записанные в конечно-разностной форме, приводятся к виду

.

(19)

Для их решения также используется метод прогонки. В этом случае расчет температурных полей  проводится по формулам

;

; ;

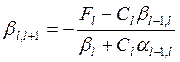, где L - номер последнего узла разностной сетки.

Рис. 4. Блок-схема расчета стационарных и динамических  характеристик ЭГК и канала холодильника-излучателя

Для вычисления коэффициентов прогонки α_i,i+1, β_i,i+1 и значений температуры в узлах разностной сетки используются граничные условия (12).

В алгоритме численного расчета были учтены условия сопряжения по потокам на границах отдельных участков ЭГЭ, полученные в подразделе 1.

Расчет распределений потенциала и плотности тока в ЭГЭ осуществлялся при заданной величине тока J , протекающего в канале. Решение интегрального уравнения для i-го ЭГЭ

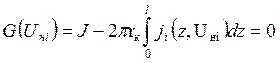
проводилось с помощью модифицированного метода Ньютона (с демпфирующим множителем a_p):

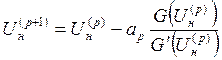, где р - номер итерации.

Следует отметить, что первоначальное значение напряжения на нагрузке U_H⁽⁰⁾задается произвольно.

Для каждого значения U_Hi разность потенциалов между электродами описывается уравнением

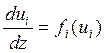, где f_i(u_i)- нелинейные функции, зависящие от величин напряжений на нагрузке U_нi. Данное уравнение решается методом простой итерации.

При табличном задании экспериментальных (или расчетных) вольтамперных характеристик изотермического и эквипотенциального ТЭП значения плотности тока в узлах разностной сетки вычисляется по формулам линейной интерполяции.

Определение электрических и тепловых характеристик ЭГК и омывающего его теплоносителя для некоторого момента времени t=πτ позволяет рассчитать температуру теплоносителя при выходе из активной зоны реактора на n-м шаге по времени. Это является исходной информацией для теплового расчета холодильника-излучателя .

Для численного интегрирования нестационарных дифференциальных уравнений (10) и (11), описывающих распределение температуры теплоносителя и стенки канала в холодильнике-излучателе, заменим их соответствующими конечно-разностными уравнениями

	(21)
	(22)

где h - шаг по оси канала, х= lh.

Для разностных уравнений (21) и (22) спектральный признак устойчивости Неймана выполняется при любом соотношении между шагами по времени и координате x . Тогда

;

,

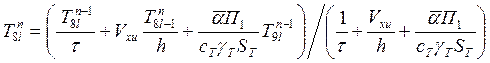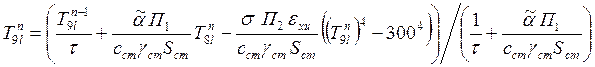, , где L=L_хи/h - количество шагов по оси канала; L_хи - длина канала.

Начальные распределения температур Т₈⁰ и Т₉⁰ задаются произвольно.

Следует отметить, что рассмотренный алгоритм определения динамических характеристик ЭГК и канала холодильника-излучателя используется и для расчета стационарного состояния системы, соответствующего заданному уровню тепловой мощности реактора. В этом случае условием завершения процесса вычислений является выполнение неравенств