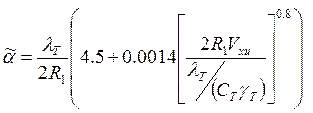Проектирование ядерной энергетической установки с многорежимными плазменными термоэмиссионными преобразователями: Учебное пособие, страница 4

- коэффициент теплоотдачи в трубке холодильника-излучателя; R₁,R₂ - внутренний и наружный радиусы канала теплоносителя; П₁=2πR₁ - внутренний периметр канала теплоносителя; П₂=(πR₂+δ_p+2q_pH_p)m - излучающий периметр канала холодильника-излучателя; λ_т(λ₇) - коэффициент теплопроводности теплоносителя;ε - степень черноты поверхности холодильника-излучателя; δ_р и Н_р - толщина и высота ребра холодильника-излучателя; m = 1...2 - количество излучающих поверхностей; q_p - безразмерный множитель, учитывающий неоднородность температуры по высоте ребра, определяется путем численного интегрирования выражения 

,

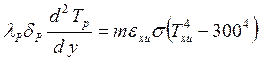где λ_р - коэффициент теплопроводности ребра.

Рассмотрим граничные условия для уравнений (1)…( 11), большинство из которых представляют собой условия сопряжения элементов ЭГК и холодильника-излучателя. При этом необходимо учитывать, что при температурах, соответствующих форсированным режимам, существенно возрастают тепловые потоки, переносимте за счёт теплопроводности в элементах катодного узла и коммутационной перемычки, поэтому требуется строгий учёт условий сопряжения.

Граничные условия для двумерного уравнения теплопроводности ядерного сердечника ЭГЭ записываются в следующем виде

(12)

Граничные условия для одномерных уравнений теплопроводности с источниками тепла в элементах ЭГК включают катод, коммуникационную перемычку и анод. Они имеют следующий вид:

(13)

где  - температура в конце анода i-го ЭГЭ, определяемая из уравнения (7) при условии

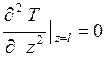
В то же время, был выполнен более точный учет условий сопряжения указанных оболочек ЭГЭ, что позволило значительно повысить адекватность данной математической модели.

Как известно, одним из условий сопряжения является равенство температур

, другим - условие баланса тепловых потоков в области сопряжения (см. рис. 2):

(14)

где

(15)

Соответствующие условия сопряжения записываются для всех граничных областей элементов ЭГЭ. Кроме того, для первого и последнего ЭГЭ канала считается, что температура токовыводов равна температуре теплоносителя на выходе Т_7вых и входе Т_7вх в активную зону, соответственно. То есть

.

Для выражения (8), представляющего распределение разности потенциалов по длине ЭГК, граничное условие определяется следующим равенством:

(16)

В качестве начального условия для момента времена t = 0 задаемся некоторым стационарным распределением температур и разности потенциалов по электрогенерирующему каналу при .

Нестационарное уравнение теплопроводности для теплоносителя в активной зоне реактора-преобразователя (9) имеет следующие начальные и граничные условия:

Т₇(0,z) = Т₇⁽⁰⁾(z); Т₇(t,0)=Т_7вых(t); Т₇(t,L_k)=Т_7вх(t)

где L_к=N(l+l_п ) - длина ЭГК.

Начальные и граничные условия для уравнений теплообмена в холодильнике-излучателе (10) и (11)

Т8(0,х) = Т8(0)(х); Т9(0,х)= Т9(0)(х); Т8(t,0)=Т7вых(t),

(17)

где Т₉(t,0) определяется из решения уравнения

(18)

Итак, задавшись геометрическими и теплофизическими параметрами элементов конструкции ЯТЭУ и имея атласы вольтамперных характеристик лабораторного ТЭП с изотермическими и эквипотенциальными электродами, с помощью системы уравнений (1…11), а также граничных и начальных условий (12…18) можно рассчитать тепловые поля, электрические и массогабаритные характеристики ЯТЭУ в стационарных и динамических режимах при заданном законе изменения во времени объемного тепловыделения в ядерном реакторе-преобразователе.

2.    Алгоритм расчета

Рассмотренные, в подразделе 1 дифференциальные и алгебраические уравнения, описывающие нестационарные процессы в реакторе-преобразователе и холодильнике-излучателе, являются нелинейными. Поэтому решение задачи может быть выполнено только с помощью численных методов. При этом алгоритм расчета переходных характеристик состоит из следующих этапов.