Полученная система является системой уравнений в форме Коши.
Из системы (5.2.1) запишем
матрицу коэффициентов, стоящих перед ![]() ,
, ![]() :
:
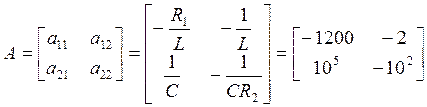 (127)
(127)

Из системы (5.2.1) запишем вектор коэффициентов, стоящих перед входными воздействиями, т. е при Е:
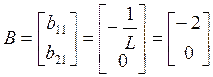 (128)
(128)
Из (5.2.1) получим матрицу-столбец входных воздействий, порядка m=1:
![]() (129)
(129)
ННУ (50) и (51) объединим в
систему, при этом учтем нашу предыдущую замену ![]() :
:
![]()
![]()
(5.2.2)
![]()
По системе (5.2.2) запишем матрицу-столбец начальных условий:
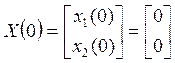 (130)
(130)
![]() (131)
(131)
Где: ![]() – матрица
искомых величин (переменных состояния),
– матрица
искомых величин (переменных состояния),
![]() – ее дифференциал.
– ее дифференциал.
Объединим (131) и () в матричную систему уравнений по переменным состояния:
![]()
![]()
(5.2.3)
![]()
5.3. Нахождение переменных состояния.
5.3.1. Определение
собственных значений ![]() .
.
Решение системы (5.3.3) представляется в виде:
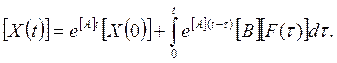 (132)
(132)
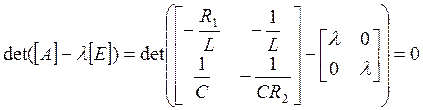 (133)
(133)
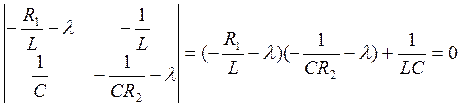 (134)
(134)
Преобразовав (134), получим характеристическое уравнение:
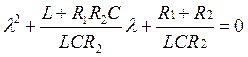 , которое имеет корни:
, которое имеет корни:![]()
5.3.2. Применение метода Рунге-Кутта для числительных расчетов.
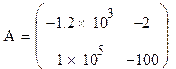 –
квадратная матрица собственных коэффициентов системы (см.(127));
–
квадратная матрица собственных коэффициентов системы (см.(127));
![]() –
вектор независимых переменных, элементы которого определяются входными
воздействиями.
–
вектор независимых переменных, элементы которого определяются входными
воздействиями.
![]() – вектор начальных условий (см.(130));
– вектор начальных условий (см.(130));
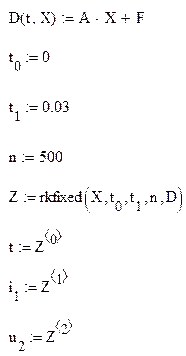
Здесь: ![]() - начальный момент переходного процесса,
- начальный момент переходного процесса, ![]() - конечный момент
переходного процесса,
- конечный момент
переходного процесса, ![]() - число шагов для численных расчетов.
- число шагов для численных расчетов.
Решение Z
представляет собой матрицу размера ![]() . Первый столбец
. Первый столбец ![]() содержит моменты времени, столбец
содержит моменты времени, столбец ![]() - значения
тока
- значения
тока ![]() ,
,![]() - значения
функции
- значения
функции ![]() ,
соответствующие этим моментам.
,
соответствующие этим моментам.
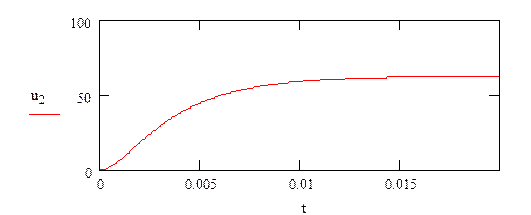
График зависимости напряжения ![]() .
.
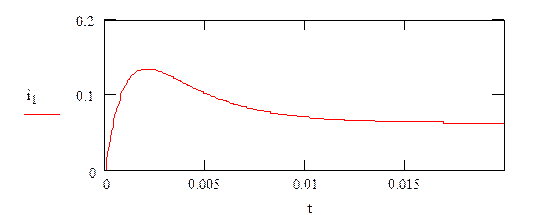
График зависимости тока ![]() .
.
Графики изменения токов i1(t), i2(t) и i3(t) приведены на рис.
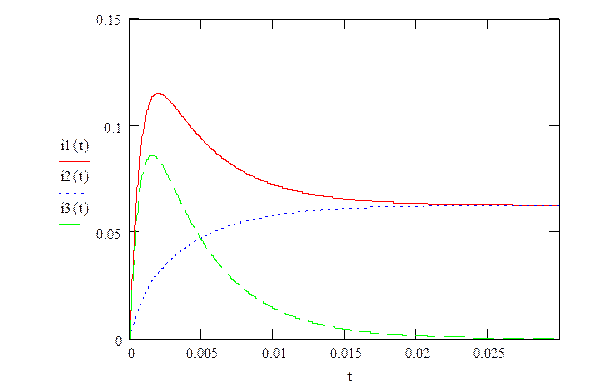
Рис.4. Графики изменения токов
Графики изменения напряжений ![]() приведены на рис.
приведены на рис.
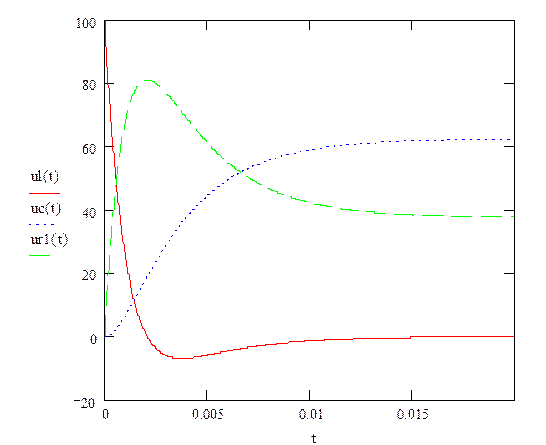
Рис.5. Графики изменения напряжений.
6.1. Проверка графиков по законам Кирхгофа.
Вычисления выполнены в программе MathCAD:
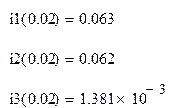
![]()
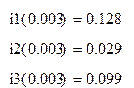
![]()
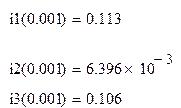
![]()
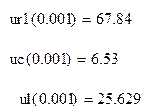
![]()
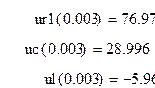
![]()
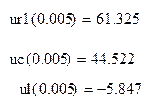
![]()
В ходе выполнения работы расчеты производились 2 методами: классическим и операторным, (кроме того, дополнительно были найдены характеристические уравнения методами переменных состояния и D-алгебраизации), которые дали одинаковые результаты:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1. Методические указания к домашним заданиям по расчету электрических цепей, под редакцией А.П.Лысенко.- Л.: ЛМИ, 1984.
2.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.