![]() (96)
(96)
Отсюда получаем:
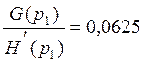 (97)
(97)
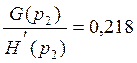 (98)
(98)
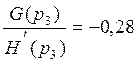 (99)
(99)

![]() (100)
(100)
Найденное решение
![]() полностью совпадает с решением, полученным
классическим методом в пункте 2.11.
полностью совпадает с решением, полученным
классическим методом в пункте 2.11.
4.7. Нахождение
операторного изображения величины ![]() .
.
Перепишем систему (4.3.1),
учитывая, что ![]() (*):
(*):
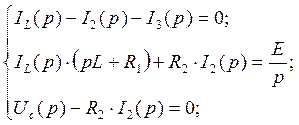
(101)
(102)
(103)
Из (101) получаем:
![]() (104)
(104)
Подставим (104) в (102):
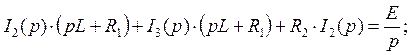
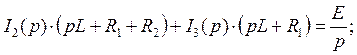 (105)
(105)
С учетом (*) (105) принимает вид:
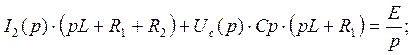 (106)
(106)
Запишем систему из уравнений (103) и (106):
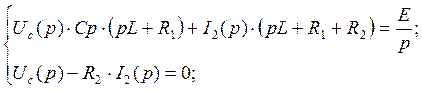
Неизвестное напряжение ![]() будем искать по формуле Крамера:
будем искать по формуле Крамера:
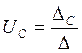
Где:
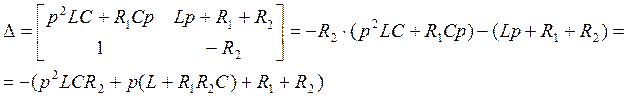 (107)
(107)
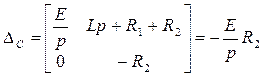 (108)
(108)
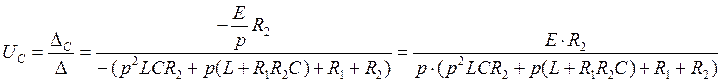
(109)
4.8. Нахождение оригинала
искомой функции ![]() .
.
Оригинал найдем по теореме разложения (88). Так как знаменатели изображений и идентичны, то корни (89) будут одинаковыми.
![]() (110)
(110)
Вычислим дроби
(соответствующие знаменатели изображений ![]() и
и ![]() равны):
равны):
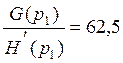 (111)
(111)
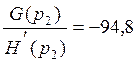 (112)
(112)
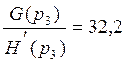 (113)
(113)

![]() (114)
(114)
Найденное решение
![]() совпадает с решением, полученным классическим
методом в пункте 2.11.
совпадает с решением, полученным классическим
методом в пункте 2.11.
Метод переменных
состояния представляет собой способ нахождения состояния системы в функции
времени, использующий матричный код решения системы дифференциальных уравнений
первого порядка, записанных в форме Коши. Под переменными состояния понимают
величины, определяющие энергетическое состояние цепи, т.е. ![]() и
и ![]() . Переменные
состояния в обобщенном смысле обозначим
. Переменные
состояния в обобщенном смысле обозначим ![]() .
.
Порядок расчета метода переменных состояния следующий:
5.1.
Составление системы уравнений по законам Кирхгофа. 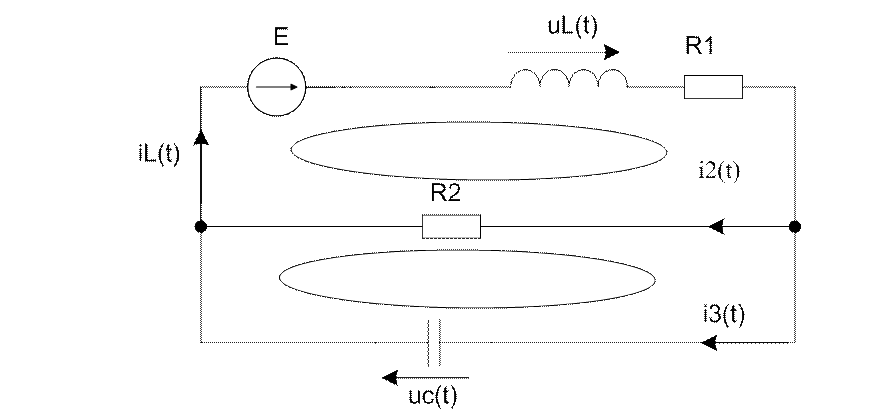
![]()
![]() (115)
(115)
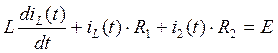 (116)
(116)
![]() (117)
(117)
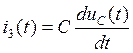 (118)
(118)
5.2. Преобразование полученной системы в систему уравнений в форме Коши относительно производных переменных состояния.
Преобразуем (115) с помощью (118):
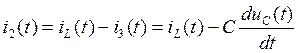 (119)
(119)
Подставим (119) в систему и получим:
![]()
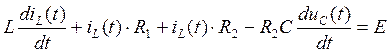 (120)
(120)
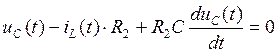 (121)
(121)
Преобразуем уравнение (121):
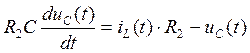 (122)
(122)
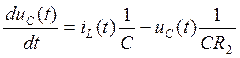 (123)
(123)
Подставим (122) в (120):
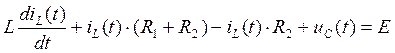
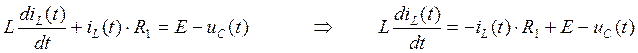
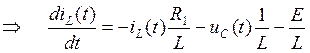 (124)
(124)
Составим систему из уравнений (123) и (124):
![]()
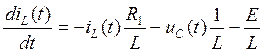 (125)
(125)
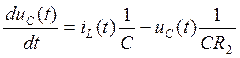 (126)
(126)
Если принять, что: 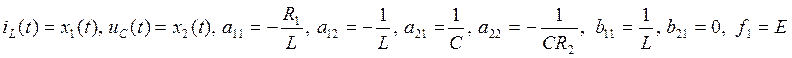
то получим:
![]()
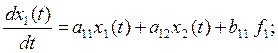
(5.2.1)
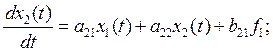
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.