Согласно второму закону коммутации напряжение на емкости до коммутации равно напряжению непосредственно после коммутации.
По законам коммутации определяем состояние катушки индуктивности и емкости в первое мгновение после начала переходного процесса:
![]() (50)
(50)
![]() (51)
(51)
Таким образом, к началу переходного процесса непосредственно перед коммутацией все токи и напряжения на пассивных элементах равны нулю, следовательно, в схеме имеют место нулевые начальные условия.
Значения
остальных токов и напряжений при ![]() в послекоммутационной схеме определяются по ННУ из
законов Кирхгофа.
в послекоммутационной схеме определяются по ННУ из
законов Кирхгофа.
Составим систему уравнений по законам Кирхгофа:
![]()
![]()
![]()
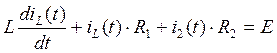 (52)
(52)
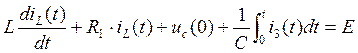
Перепишем систему (52) для момента времени t=0, учитывая ННУ (50) и (51):
![]()
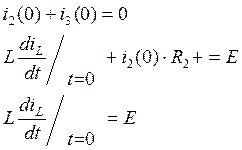 (53)
(53)
Преобразовав систему (53), получим:
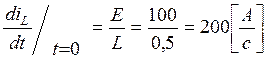 ; (54)
; (54)
![]()
![]() (55)
(55)
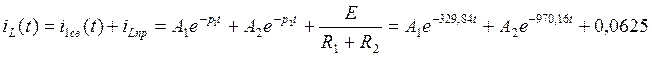
(56)
В выражении (56) неизвестными являются только постоянные интегрирования.
Определим постоянные интегрирования А1 и А2, исходя из начальных условий:
ННУ:
При t=0:
![]() (57)
(57)
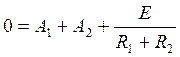 (58)
(58)
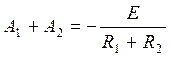 (59)
(59)
![]()
ЗНУ:
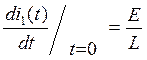
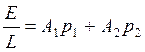 (60)
(60)
![]()
 (61)
(61)
Используя (59) и (61), имеем:
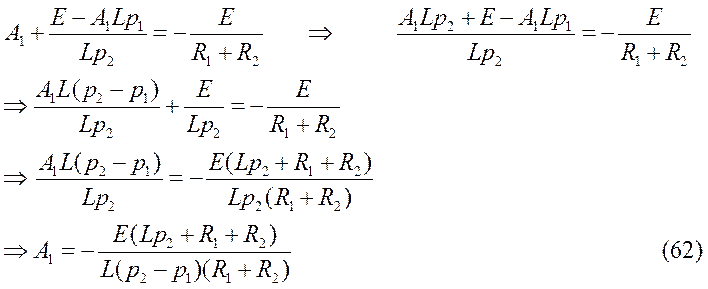
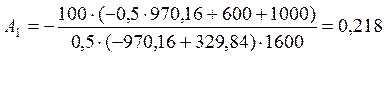
Подставляем А1 в (61) и находим А2:
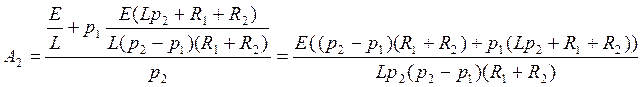 (63)
(63)
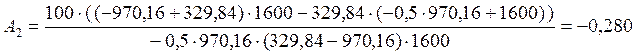
· Подставляя А1 и А2 в (56), получим:
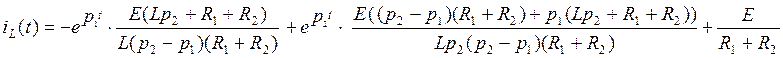
![]() (64)
(64)
![]()
·
Напряжение на катушке
индуктивности найдем с помощью уравнения связи 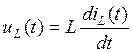 :
:
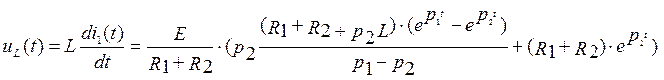
![]()
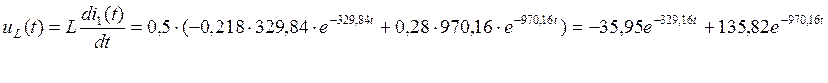 (65)
(65)
·
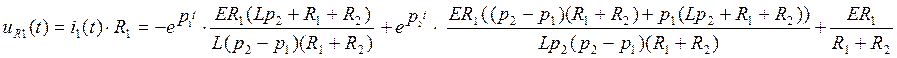
![]()
(66)
·
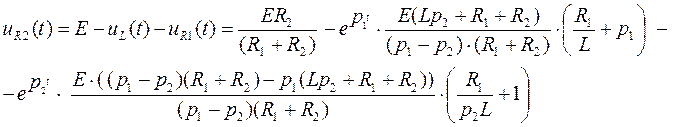
![]()
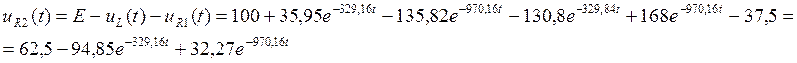
(67)
·
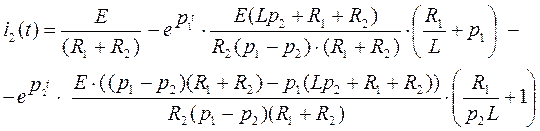
![]()
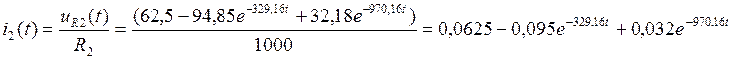
(68)
·
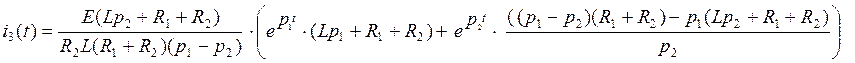
![]()
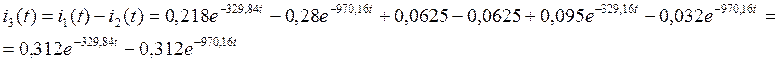 (69)
(69)
·
![]() (70)
(70)
![]()
Величины |
Расчетная формула |
|
|
|
iL(t), A |
|
0 |
|
|
i2(t),A |
|
0 |
|
|
i3(t),A |
|
0 |
|
|
uR1(t),B |
|
0 |
|
|
uR2(t),B |
|
0 |
|
|
uL(t),B |
|
0 |
|
|
uС(t),B |
|
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.