Перерисуем схему на рис.1 в момент коммутации – рис.2.
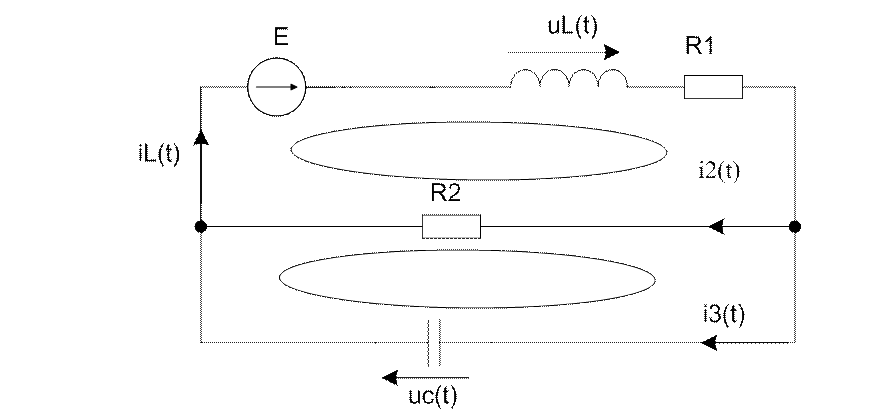
Рис.2
Исходная система уравнений (1.1) для момента времени после коммутации содержит 3 уравнения, записанные по законам Кирхгофа, и одно уравнение связи:
![]()
![]() (2)
(2)
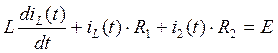 (3)
(1.1)
(3)
(1.1)
![]() (4)
(4)
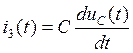 (5)
(5)
Степень дифференциального и характеристического уравнений (12)-(13) относительно тока iL(t) равна числу основных ННУ в схеме, т.е. порядок равен двум (катушка индуктивности и емкость).
Тогда систему уравнений (1.1) сведем к одному дифференциальному уравнению второго порядка относительно тока iL(t).
Выразим ![]() через
через ![]() , воспользовавшись
(3) и (4):
, воспользовавшись
(3) и (4):
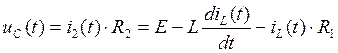 (6)
(6)
Продифференцируем (6) но t:
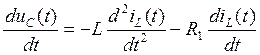 (7)
(7)
Выразим ![]() из (4),
подставим в (2) и найдем
из (4),
подставим в (2) и найдем ![]() :
:
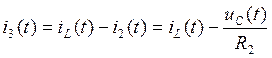 (8)
(8)
Подставим (8),(7) и (6) в (5):
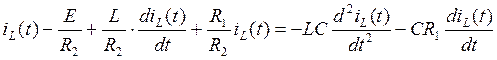 (9)
(9)
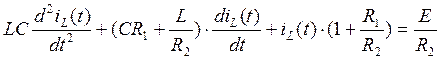 (10)
(10)
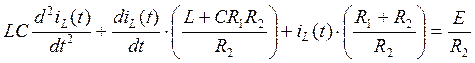 (11)
(11)

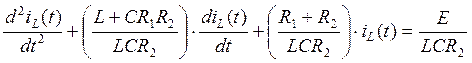 (12)
(12)
Физический смысл
свободной составляющей – описание поведения системы при отсутствии внешнего
воздействия. Уравнение (12) – линейное неоднородное дифференциальное уравнение
второго порядка, общий интеграл которого есть сумма частного решения неоднородного
уравнения, полученного в форме правой
части для неоднородного уравнения (принужденная составляющая силы тока) плюс общее решение однородного уравнения (свободная составляющая силы тока). Для получения
однородного дифференциального уравнения
необходимо в (12) свободный член 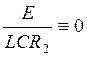 , т.е.
, т.е.
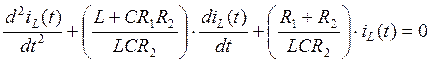
Теперь заменим соответственно
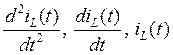 на
на ![]() и получим характеристическое
уравнение:
и получим характеристическое
уравнение:
 |
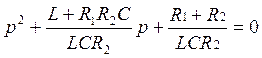 (13)
(13)
Наиболее простой способ составления характеристического уравнения цепи состоит в следующем:
2.3.1. Записывают формулу входного сопротивления цепи в комплексной форме
В цепи на рис.2 сопротивления ![]() и
и
![]() включены параллельно:
включены параллельно:
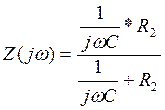 (14)
(14)
С учетом (14) полное сопротивление цепи принимает вид:
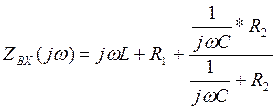 (15)
(15)
2.3.2. В формуле (14)
произведем замену сомножителя ![]() на
на ![]() :
:
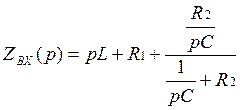 (16)
(16)
2.3.3. Полученное
выражение приравняют нулю ![]() :
:
Приравняв (16) нулю, получаем:
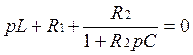 (17)
(17)
Преобразуем (17):
![]() (18)
(18)

![]() (19)
(19)
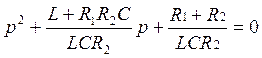 (20)
(20)
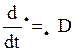 (21)
(21)
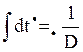 (22)
(22)
Исходная система уравнений,
составленная по законам Кирхгофа c учетом
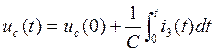 , имеет следующий вид:
, имеет следующий вид:
![]()
![]()
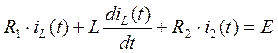
![]() (23)
(23)
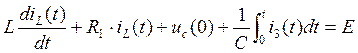
Преобразуем систему с помощью (21) и (22):
![]()
![]() `
(24)
`
(24)
![]() (25)
(25)
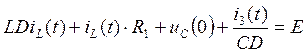 (26)
(26)
Выразим ![]() из (24) и
подставим в (25):
из (24) и
подставим в (25):
![]()
![]() (27)
(27)
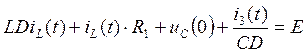 (28)
(28)
![]()
![]() (29)
(29)
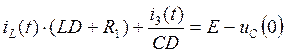 (30)
(30)
Неизвестный ток ![]() можно найти
по формуле Крамера:
можно найти
по формуле Крамера:
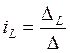
Где:
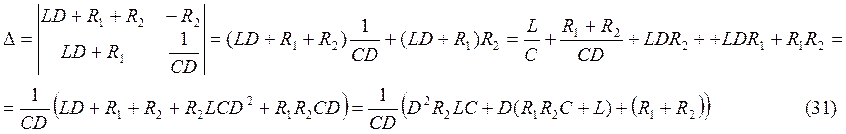
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.