¾ определитель системы,
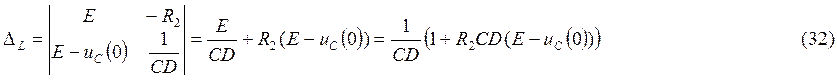
¾
определитель, полученный из
определителя ![]() путем
замены первого столбца коэффициентов столбцом из свободных членов.
путем
замены первого столбца коэффициентов столбцом из свободных членов.
Подставим определители ![]() и
и ![]() в формулу
Крамера:
в формулу
Крамера:
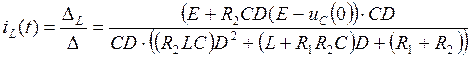 (33)
(33)
![]() (34)
(34)
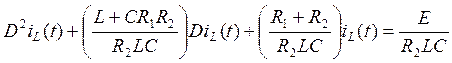 (35)
(35)
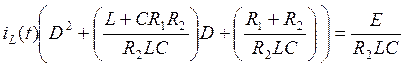 (36)
(36)
Выполнив обратную замену 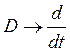 и
и 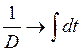 ,
получим линейное дифференциальное уравнение:
,
получим линейное дифференциальное уравнение:

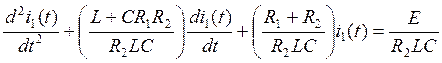 (37)
(37)
Приравняв правую часть уравнения (36) нулю, получим характеристическое уравнение, аналогичное (13):
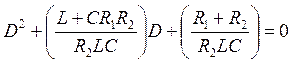 (38)
(38)
Найдем корни характеристического уравнения, полученного ранее различными способами
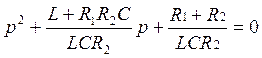
Для облегчения расчетов сделаем замену и перепишем характеристическое уравнение следующим образом::
![]() (39)
(39)
Где:
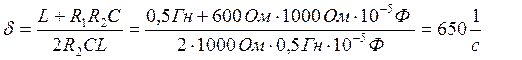
¾ коэффициент затухания колебаний в контуре;
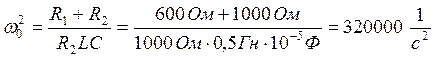
Откуда:
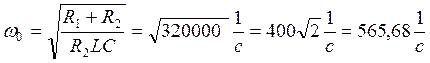
¾ угловая частота незатухающих колебаний;
Проверим
размерность ![]() и
и
![]() , для этого
в формулах заменим элементы их размерностями. При этом учтем, что:
, для этого
в формулах заменим элементы их размерностями. При этом учтем, что:
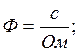
![]()
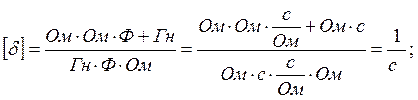
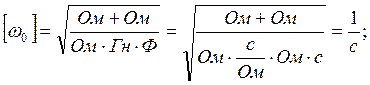
Из
(39) следует, что корни характеристического уравнения имеют размерность ![]() и рассчитываются
по формуле:
и рассчитываются
по формуле:
![]() (40)
(40)
Так как ![]() , корни
вещественные отрицательные:
, корни
вещественные отрицательные:
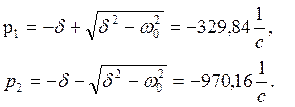 (41)
(41)
Выражение
свободной составляющей силы тока определяется видом корней характеристического
уравнения (13). Так как корни ![]() и
и ![]() вещественные,
выражение свободной силы тока имеет вид:
вещественные,
выражение свободной силы тока имеет вид:
![]() (42)
(42)
Уравнение (42) физически определяет поведение цепи при отсутствии внешних источников электрической энергии.
Установившийся
режим работы цепи обусловлен действием источников энергии, поэтому принужденная
составляющая ![]() в
случае постоянного напряжения
в
случае постоянного напряжения ![]() может быть найдена методами расчета установившегося процесса в цепи
после коммутации. В схеме, изображенной на рис. 2 закоротим индуктивность (
может быть найдена методами расчета установившегося процесса в цепи
после коммутации. В схеме, изображенной на рис. 2 закоротим индуктивность (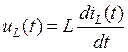 – при постоянном токе напряжение на катушке не
изменяется) и разорвем ветвь с емкостью – нарисована пунктирной линией (
– при постоянном токе напряжение на катушке не
изменяется) и разорвем ветвь с емкостью – нарисована пунктирной линией (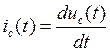 – при постоянном напряжении ток в ветви с конденсатором
равен нулю
– при постоянном напряжении ток в ветви с конденсатором
равен нулю ![]() ), таким образом, в цепи на рис.3 все установившиеся
токи и напряжения не будут зависеть от времени.
), таким образом, в цепи на рис.3 все установившиеся
токи и напряжения не будут зависеть от времени.
Рис.3.
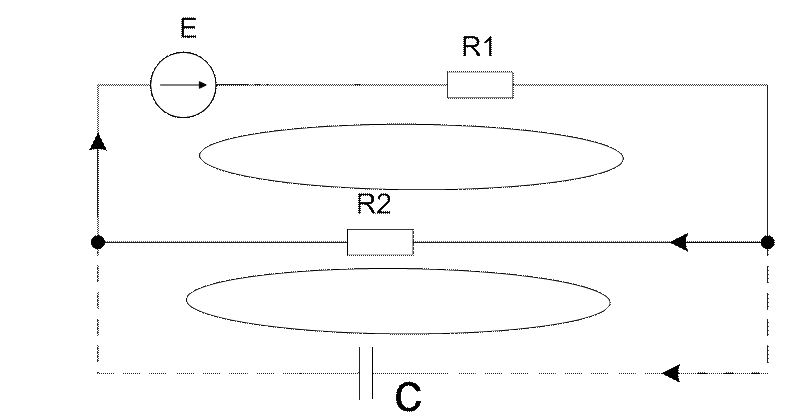
По второму закону Кирхгофа (рис.3) после коммутации:
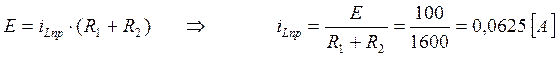 (43)
(43)
Тот же результат получаем, если в уравнении (12) учесть, что производная от константы равна нулю:

Теперь найдем принужденные составляющие остальных токов и напряжений:
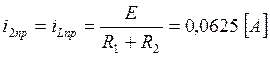 (44)
(44)
![]() (45)
(45)
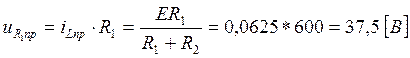 (46)
(46)
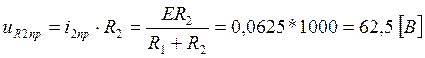 (47)
(47)
![]() (48)
(48)
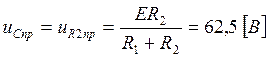 (49)
(49)
Независимые
начальные условия определяются количеством реактивных накопителей энергии в
схеме. Состояние каждого накопителя может быть охарактеризовано либо текущим
через него током, либо падением напряжения на нем. Независимыми переменными
являются: для емкости – напряжение на ней ![]() , для индуктивности – ток через нее
, для индуктивности – ток через нее ![]() .
.
Определим независимые начальные условия. Для этого найдем ток в индуктивности и напряжение на емкости до коммутации. Так как до коммутации ключ в ветви с источником ЭДС был разомкнут, то:
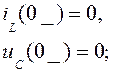
Согласно первому закону коммутации ток через
индуктивность непосредственно до коммутации ![]() равен току через ту же индуктивность
после коммутации
равен току через ту же индуктивность
после коммутации ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.