величины |
|
|
||
|
По З.К. |
По расчетным уравнениям |
По З.К. |
По расчетным уравнениям |
|
|
i1(t), A |
0 |
0,0005 |
|
0,0625 |
|
i2(t),A |
0 |
0,0001 |
|
0,0625 |
|
i3(t),A |
0 |
0 |
0 |
0 |
|
uR1(t),B |
|
0,21 |
|
37,5 |
|
uR2(t),B |
|
0,02 |
|
62,5 |
|
uL(t),B |
|
99,87 |
0 |
0 |
|
uС(t),B |
0 |
0,02 |
|
62,5 |
Более удобным методом решения линейных дифференциальных уравнений является операторный метод, так как в нем не требуется дополнительно определять постоянные интегрирования.
Порядок расчета цепей операторным методом состоит в следующем:
Воспользуемся начальными условиями, определенными в пункте 2.8.А:
![]() (71)
(71)
![]() (72)
(72)
В схему для
изображений последовательно с индуктивностью включается дополнительный источник
ЭДС, совпадающий с положительным направлением тока, равный ![]() ; а
последовательно с емкостью – дополнительный источник ЭДС, противоположно
направленный с тока положительным направлением тока в ветви, равный
; а
последовательно с емкостью – дополнительный источник ЭДС, противоположно
направленный с тока положительным направлением тока в ветви, равный 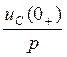 .
.
Операторная схема
замещения приведена на рис. 4. 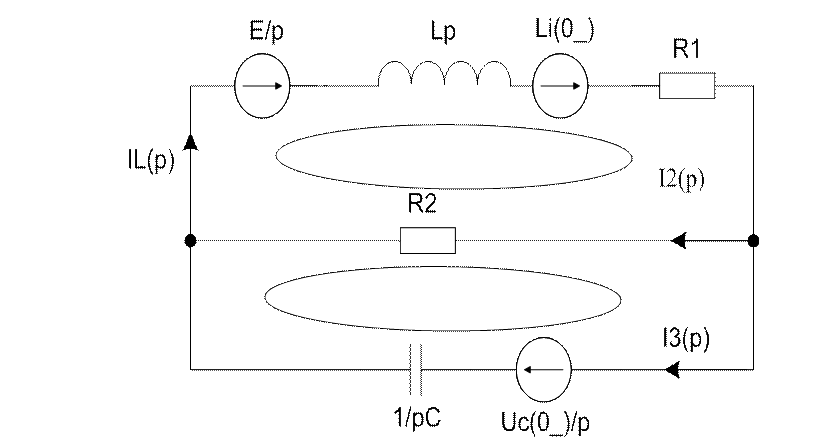
Рис. 4. Операторная схема замещения.
Запишем систему уравнений по законам Кирхгофа в операторном виде:
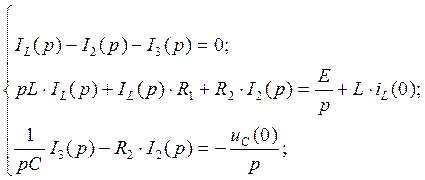
(73)
(74)
(75)
Перепишем систему с учетом (71) и (72):
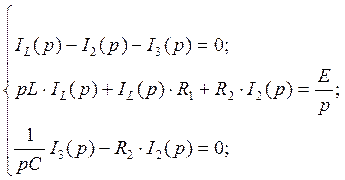
(76)
(77) (4.3.1)
(78)
Из (77) получаем:
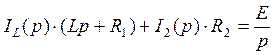 (79)
(79)
Из (76):
![]() (80)
(80)
Преобразуем (78) с учетом (80):
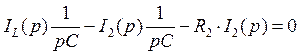 (81)
(81)
Мы получаем систему из уравнений (79) и (81):
![]()
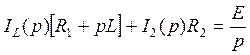 (82)
(82)
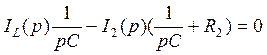 (83)
(83)
4.5. Нахождение
операторного изображения величины ![]() .
.
Неизвестный ток ![]() можно найти по формуле Крамера:
можно найти по формуле Крамера:
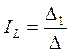
Где:
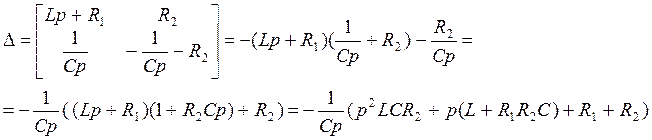 (84)
(84)
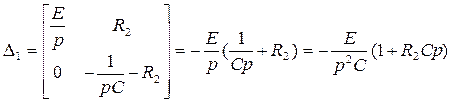 (85)
(85)
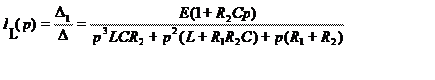 (86)
(86)
4.6. Нахождение оригинала
искомой функции ![]() .
.
Решение ![]() представим
в виде отношения двух полиномов оператора
представим
в виде отношения двух полиномов оператора ![]() :
:
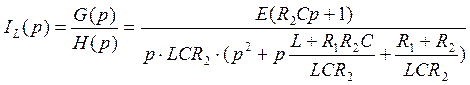 (87)
(87)
По теореме разложения находим
оригинал-закон изменения ![]() :
:
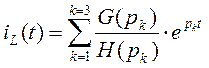 (88)
(88)
В нашем случае:

![]()
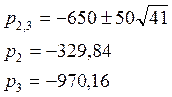 (89)
(89)
![]() (90)
(90)
![]() (91)
(91)
![]() (92)
(92)
![]() (93)
(93)
![]() (94)
(94)
![]() (95)
(95)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.