


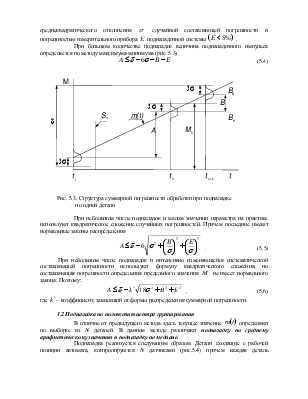







Лабораторная работа № 5 .
Цель работы: изучение методов автоподналадки технологического оборудования, экспериментальное определение основных параметров подналадки.
1. Методические указания к выполнению лабораторной работы
Влияние систематических и случайных факторов в процессе обработки партии деталей на автоматическом оборудовании обуславливает необходимость периодической автоматической подналадки, поскольку затраты времени на ручную подналадку составляют около 20% рабочего времени или 75% времени простоя оборудования.
Работа технологического оборудования снабженного системой подналадки иллюстрируется с помощью рис. 5.1. Здесь параметры деталей нанесены на график в порядке хронологической последовательности обработки их на автомате.
Линия ![]() называется линией
изменения усредненных погрешностей и характеризует систематическую составляющую
изменения погрешностей деталей.
называется линией
изменения усредненных погрешностей и характеризует систематическую составляющую
изменения погрешностей деталей.
Отклонения погрешностей деталей центрированы
относительно ![]() и характеризуются, как правило,
нормальным законом распределения с дисперсией
и характеризуются, как правило,
нормальным законом распределения с дисперсией ![]() и
среднеквадратическим отклонением
и
среднеквадратическим отклонением ![]() .
.
При
достижении определенного значения ![]() , срабатывает
система автоподналадки, которая изменяет настройку оборудования на величину
подналадочного импульса A. Во время подналадки изделия не обрабатываются.
, срабатывает
система автоподналадки, которая изменяет настройку оборудования на величину
подналадочного импульса A. Во время подналадки изделия не обрабатываются.
Предельное значение ![]() меньше верхней границы поля допуска
на
меньше верхней границы поля допуска
на ![]() , однако включить подналадку в этот
момент невозможно, т. к. определение текущего значения
, однако включить подналадку в этот
момент невозможно, т. к. определение текущего значения ![]() производиться
среднестатистическим методом по определенной выборке деталей. Поэтому точка
срабатывания «b» (рис.5.1) располагается в некоторой зоне
подналадки B , а период
времени между подналадками является переменной величиной.
производиться
среднестатистическим методом по определенной выборке деталей. Поэтому точка
срабатывания «b» (рис.5.1) располагается в некоторой зоне
подналадки B , а период
времени между подналадками является переменной величиной.
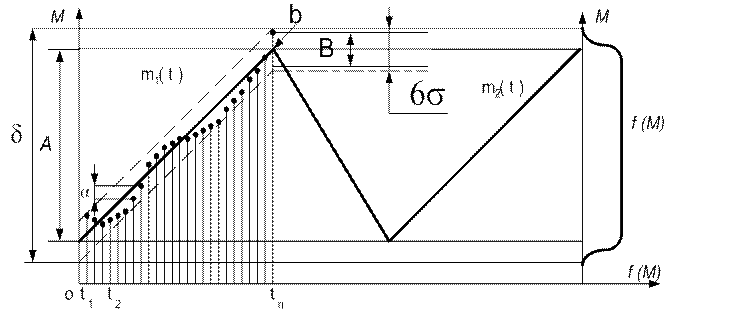
Рис. 5.1. Изменения выходного параметра в процессе обработки
Системы автоподналадки компенсируют лишь
систематические составляющие погрешности и не устраняют влияние собственно
случайных составляющих погрешностей. Анализ точности подналадочных систем
производится на основе метода скользящей средней. При этом считают, что
погрешности подчиняются нормальному закону распределения, а функция ![]() имеет линейный характер.
имеет линейный характер.
1.1. Метод автоподналадки по одной детали
Процесс подналадки в соответствии с данным
методом реализуется следующим образом. Предельный датчик настроенный на уставку
![]() , последовательно контролирует
все детали, сходящие с рабочей позиции автомата. Если величина параметра
, последовательно контролирует
все детали, сходящие с рабочей позиции автомата. Если величина параметра ![]() какой-либо детали превысит
величину
какой-либо детали превысит
величину ![]() , то система перестраивается
на величину подналадочного импульса A.
, то система перестраивается
на величину подналадочного импульса A.
Оценим точные характеристики метода. Как
следует из рис. 5.2, вероятность подналадки ![]() возникает
практически при контроле
возникает
практически при контроле ![]() - й детали, если
пренебречь вероятностью меньшей 0,00134. Центр группирования
- й детали, если
пренебречь вероятностью меньшей 0,00134. Центр группирования ![]() в этот момент определяет положение
нижней границы
в этот момент определяет положение
нижней границы ![]() зоны
подналадки
зоны
подналадки ![]() . Так как события подналадки и
неподналадки являются противоположными, то вероятность неподналадки в момент времени
. Так как события подналадки и
неподналадки являются противоположными, то вероятность неподналадки в момент времени
![]() равна
равна
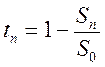 ,
,
где
![]() - номер детали;
- номер детали; ![]() - часть площади
- часть площади ![]() дифференциального закона
распределения отсекаемая на уровне
дифференциального закона
распределения отсекаемая на уровне ![]() .
.
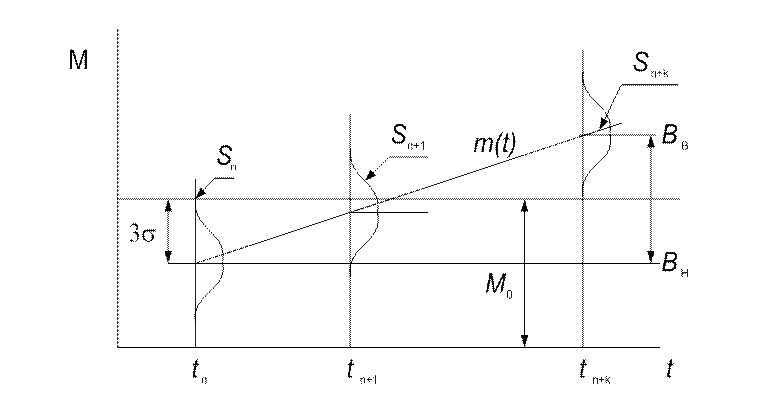
Рис. 5.2. К определению вероятности подналадки по одной детали
Если подналадка в момент ![]() не произойдет, то вероятность
неподналадок в моменты времени
не произойдет, то вероятность
неподналадок в моменты времени ![]() ,
, ![]() , …,
, …, ![]() можно
определить как вероятности сложных событий, используя закон умножения
независимых вероятностей. Тогда вероятность неподналадки в момент времени
можно
определить как вероятности сложных событий, используя закон умножения
независимых вероятностей. Тогда вероятность неподналадки в момент времени ![]() можно выразить следующим образом
можно выразить следующим образом
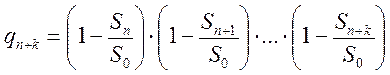 . (5.1)
. (5.1)
Как следует из выражения (1), вероятность
неподналадки при увеличении ![]() уменьшается.
Поэтому определив
уменьшается.
Поэтому определив ![]() , начиная с которого
вероятность неподналадки практически равна нулю
, начиная с которого
вероятность неподналадки практически равна нулю ![]() ,
а вероятность подналадки
,
а вероятность подналадки ![]() ,можно
установить положение верхней границы
,можно
установить положение верхней границы ![]() зоны подналадки
зоны подналадки
![]() .
.
Если предположить, что систематическая
составляющая погрешности изменяется линейно, причем величина изменения ее за
время изготовления одной детали равна ![]() ,
то ширина зоны
,
то ширина зоны
![]() (5.2)
(5.2)
Таким образом, зная величину
приращения ![]() и определив по формуле (5.1)
значение
и определив по формуле (5.1)
значение ![]() , можно вычислить ширину зоны
подналадки
, можно вычислить ширину зоны
подналадки ![]() .
.
Величины отношений 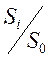 можно
определить по интегралу вероятностей
можно
определить по интегралу вероятностей 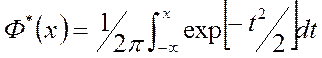 табулированные
значения которого приведены на лабораторном макете
табулированные
значения которого приведены на лабораторном макете
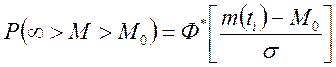 .
.
Пример.
Дано: ![]() . Определить ширину зоны
подналадки
. Определить ширину зоны
подналадки ![]() . Практически вероятность подналадки
возникает при
. Практически вероятность подналадки
возникает при ![]() , т.е.
, т.е. ![]() . Тогда
. Тогда 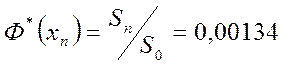 .
Рассчитывая последовательно значения
.
Рассчитывая последовательно значения ![]() ,
, ![]() , …,
, …,![]() в
соответствии с соотношением (1) вычислим вероятность неподналадки
для разных
в
соответствии с соотношением (1) вычислим вероятность неподналадки
для разных ![]()
![]()
Получим, что![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
т.е. начиная с
,
т.е. начиная с ![]() , вероятность подналадки
практически равна 1 , а искомая величина зоны подналадки
, вероятность подналадки
практически равна 1 , а искомая величина зоны подналадки ![]() .
.
При ![]() такой
способ определения зоны подналадки
такой
способ определения зоны подналадки ![]() становится трудоемким,
так как с увеличением
становится трудоемким,
так как с увеличением ![]() а растет
а растет ![]() . Поэтому на практике используют
приближенное значение
. Поэтому на практике используют
приближенное значение
![]() (5.3)
(5.3)
где
![]() ;
; ![]() – выражается в единицах
среднеквадратического отклонения
– выражается в единицах
среднеквадратического отклонения ![]() .
.
При указанных ранее ограничениях суммарное
распределение выходного параметра ![]() партии деталей
будет представлять собой композицию законов Гаусса и равной вероятности
партии деталей
будет представлять собой композицию законов Гаусса и равной вероятности ![]() (рис.5.1).
(рис.5.1).
Величина подналадочного импульса ![]() определяется положением зоны подналадки
определяется положением зоны подналадки
![]() , полем допуска
, полем допуска ![]() контролируемого параметра
контролируемого параметра ![]() , величиной среднеквадратического
отклонения
, величиной среднеквадратического
отклонения ![]() случайной составляющей погрешности и
погрешностью измерительного прибора
случайной составляющей погрешности и
погрешностью измерительного прибора ![]() подналадочной
системы
подналадочной
системы ![]() .
.
При большом количестве подналадок величина подналадочного импульса определяется по методу максимума-минимума (рис. 5.3)
![]() .
(5.4)
.
(5.4)
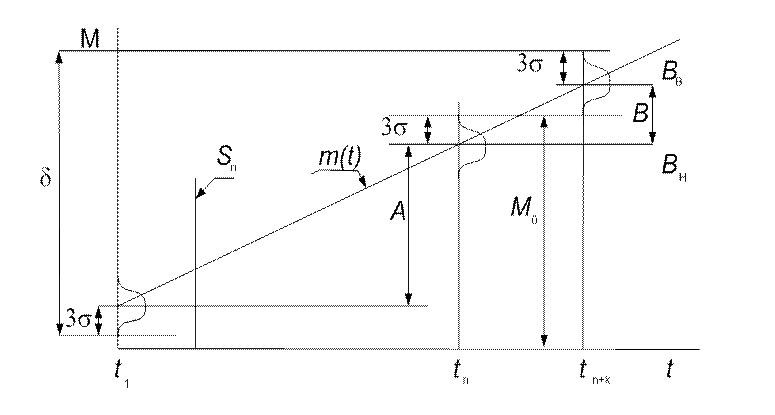
Рис. 5.3. Структура суммарной погрешности обработки при подналадке
по одной детали
При небольшом числе подналадок и малом значении параметра на практике используют квадратическое сложение случайных погрешностей. Причем последние имеют нормальные законы распределения
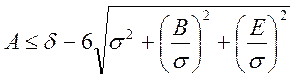 . (5.5)
. (5.5)
При небольшом числе подналадок и интенсивно
изменяющейся систематической составляющей погрешности используют формулу
квадратического сложения, но составляющая погрешности определения предельного
значения ![]() не имеет нормального закона. Поэтому:
не имеет нормального закона. Поэтому:
![]() , (5.6)
, (5.6)
где
![]() – коэффициент, зависящий от формы
распределения суммарной погрешности.
– коэффициент, зависящий от формы
распределения суммарной погрешности.
1.2 Подналадка по положению центра группирования
В отличие от предыдущего метода здесь
текущее значение ![]() определяют по выборке из N деталей. В данном методе различают подналадку по среднему
арифметическому значению и подналадку по медиане.
определяют по выборке из N деталей. В данном методе различают подналадку по среднему
арифметическому значению и подналадку по медиане.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.