Изучение методов автоподналадки технологического оборудования, экспериментальное определение основных параметров подналадки, страница 2

            Подналадка реализуется следующим образом. Детали сходящие с рабочей позиции автомата, контролируются N датчиками (рис.5.4) причем каждая деталь последовательно проходит все датчики, настроенные на установку . Датчики контролируют величину и знак отклонения параметра соответствующей детали от .

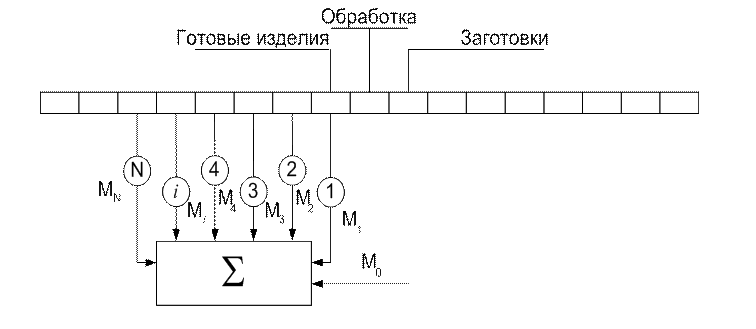
Рис. 5.4. Схема подналадки по положению центра группирования

            Если используется метод среднего арифметического, то отклонения алгебраически складываются в сумматоре. Когда их сумма станет равной нулю, срабатывает система автоподналадки и перестраивает оборудование.

            Если используется метод медианы, то отклонения необходимо суммировать с определенными весами. Однако на практике используют упрощенный метод: контролируется только знак и число отклонений

            Для срабатывания системы автоподналадки достаточно, чтобы число положительных отклонений от  равнялось числу отрицательных отклонений. Количество датчиков в этом случае должно быть четным.

            Найдем оценку  для метода среднего арифметического. Поскольку в заданный момент времени датчики контролируют N деталей, то в результате имеется N случайных значений параметров , , … ,.

            В связи с тем, что систематическая составляющая погрешности  является линейной возрастающей функцией, то среднее арифметическое значение всегда меньше . А сами значения, пронумерованные от рабочей позиции автомата, отличаются на величину ,  , т.е.,  где - центрированная случайная величина, подчиняющаяся нормальному закону распределения с дисперсией .

            При этом для  можно предложить следующую оценку:

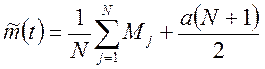  ,                                                 (5.7)

Проверка состоятельности и несмещенности оценки  сводится к определению ее математического ожидания

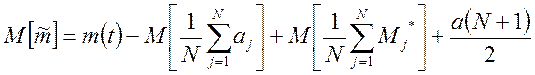 .                            (5.8)

            В полученном выражении второе слагаемое представляет собой сумму арифметической прогрессии и его модуль равен четвертому слагаемому, третье же слагаемое равно нулю.

            В результате имеем:

                                           .                                                            (5.9)

            Таким образом, оценка является состоятельной и несмещенной.

            Определим дисперсию оценки. В соотношении (5.8) три слагаемых являются постоянными и их дисперсии равны нулю. Поэтому дисперсия оценки будет равна дисперсии суммы случайных величин

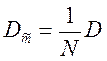   .                                                               (5.10)

            Величина зоны подналадки  в этом случае будет определяться доверительным интервалом  с центром в точке  и длиной ,  который накроет точку  c вероятностью   т.е.

  .                                                (5.11)

             

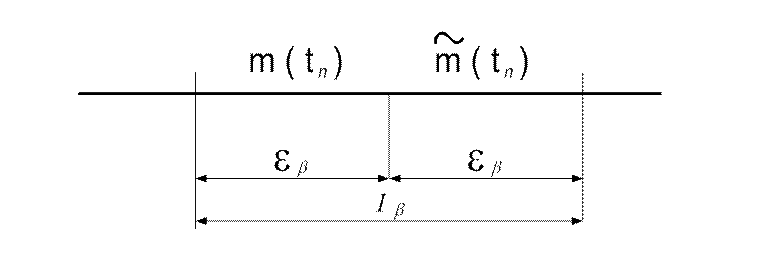
Рис. 5.5. К определению доверительного интервала

Для определения длины доверительного интервала учтем, что оценка представляет собой сумму N независимых, распределенных по нормальному закону случайных величин  и , следовательно, сама является случайной величиной, распределенной по нормальному закону с математическим ожиданием (5.9) и дисперсией (5.10).

            В этом случае для определения   можно использовать функцию Лапласа [3]

. Откуда длина доверительного интервала выразится соотношением

   ,

где     - квантиль нормального распределения, т.е. такое значение аргумента, для которого функция Лапласа равна .   В частности для    ,      .

  Так как разница между оценкой и оцениваемой величиной в выражении   (11) берется по абсолютной величине, то величина зоны подналадки с заданной вероятностью  будет равна двум доверительным интервалам

  .

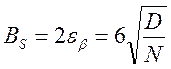На практике обычно N= 4…6. Использование упрощенного метода медианы дает большее значение зоны подналадки

  .

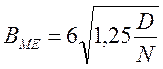Однако эта разновидность метода менее чувствительна к грубым ошибкам, в то время как оценка  менее критична к искажениям закона распределения.

   Но при выборе установки следует учесть, что до сих пор рассматривались абсолютные значения оценки, в то время как метод реализуется с использованием отклонений от уставки. Поэтому для правильного расположения зоны подналадки уставка должна быть выбрана в соответствии с рис. 5.6.

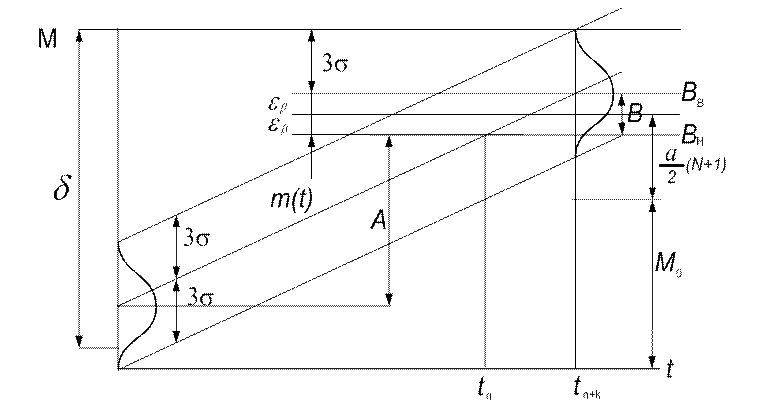
Рис. 5.6. Структура суммарной погрешности обработки при наладке по

             центру группирования

            Суммарная погрешность рассмотренного метода имеет ту же структуру, что и погрешность подналадки по одной детали. Поэтому можно использовать формулы (5.4), (5.5), (5.6), подставляя в них вместо  величины (5.12), (5.13), а вместо погрешности контрольного устройства 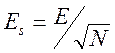  или  .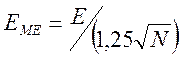

2. Описание лабораторной установки

Лабораторная работа выполняется  в учебной вычислительной лаборатории на сетевых  ЭВМ  в ППП MS Excel.

3. Порядок выполнения работы

Выполнение лабораторной работы основывается на статистическом моделировании технологического процесса изготовления деталей с помощью вейерной модели. Пример оформления лабораторной работы приведен в «Заданиях 5.1., 5.2., 5.3 » в ППП MS Excel.

3.1.  Моделирование автоподналадки по одной детали

Моделирование технологического процесса изготовления деталей осуществляется в следующем порядке «Задание 5.1.» :

1. В ячейки А4-А53 записывают номера изготавливаемых деталей от 1 до 50.

2.  В  ячейки В4-В53 и С4-С53 записывают случайные числа с помощью датчика случайных чисел с равномерным законом распределения [0,1] - СЛЧИС().

3. В  ячейки D4-D53 и E4-E53 записывают значения центрированной случайной величины - случайные числа с нормальным законом распределения на основе прямого метода моделирования (m = 0, )( см. Задание 1.4.).

4. В  ячейках С, D, E 54-59 рассчитывают оценки математического ожидания, дисперсии, среднеквадратического отклонения, половины поля рассеяния, минимального и максимального значений массивов  В4-С53, D4-D53 и E4-E53 (см. Задание 1.1.).

5. В  ячейках F4-F53 моделируют, рассчитывая значения случайной функции изменения параметра М в процессе изготовления деталей («Ряд параметров»); где  - начальное значение настройки процесса (М = 3);   -  значение среднего приращения параметра М от детали к детали (а = 0,4);   - номер изготавливаемой детали (ячейки А4-А53);  - среднеквадратическое отклонение центрированной случайной величины (ячейка Е56); - значения центрированной случайной величины по нормальному закону распределения (ячейки D4-D53).

6. В  ячейках G5-G53 рассчитывают случайные величины приращений параметра М «Ряд приращений» .

7. В  ячейках G54-G59 рассчитывают статистические оценки «Ряда приращений».

8. В  ячейках Н4-Н53 рассчитывают отношение величины параметра  к величине уставки -   -  , где  – величина допуска - процент максимального отклонения параметра М .