Изучение методов автоподналадки технологического оборудования, экспериментальное определение основных параметров подналадки, страница 3

9. В  ячейках I4-I53 записывают результат округления величины отношения в ячейках Н4-Н53. Если величины округленной величины в ячейках I4-I53 равен 0, то случайная величина  не достигла уставки , при равенстве кругленной величины 1, величина  превышает величину уставки и, при этом требуется подналадка оборудования.

10. Величины «Ряда параметров» и округленной величины сравнения с уставкой выводят на график.

11. Определяют номер детали с которой следует произвести наладку.

12. Определяют текущую величину параметра  детали с которой следует производить наладку.

         3.2. Моделирование подналадки по положению центра группирования

Моделирование подналадки по положению центра группирования технологического процесса изготовления осуществляется в следующем порядке «Задание 5.2.» :

1. Выполняют моделирование технологического процесса изготовления деталей, аналогично п. 3.1. (1,2,3,4,5,6,7 );

2. В ячейках Н4-Н53 определяют отклонение значений параметра  от величины уставки -   -  , где  – величина допуска - процент максимального отклонения параметра М;

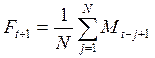3. В ячейках I9-I53 рассчитывают скользящее среднее для 5-и предыдущих значений  по формуле , где ;

4. В ячейках J9-J53 вычисляют величину знака отклонения величины скользящего среднего от величины уставки ;

5. Определяют номер детали, для которой величина скользящего среднего будет равна 0, при этом величина достигнет величины уставки , а знак величины скользящего среднего изменится с «-» на «+»;

6. Величины «Ряда параметров» и знака  отклонения величины скользящего среднего от величины уставки  выводят на график;

11. Определяют номер детали с которой следует произвести наладку;

12. Определяют текущую величину параметра  детали с которой следует производить наладку.

         3.3. Сравнительный анализ моделей подналадки по одной детали и по        

                положению центра группирования

Сравнительный анализ моделей подналадки по одной детали и по положению центра группирования технологического процесса изготовления деталей, а также сравнение с методом подналадки по методу медианы,   осуществляется в следующем порядке «Задание 5.3.» :

1. Выполняют моделирование технологического процесса изготовления деталей, аналогично п. 3.1. (1,2,3,4,5,6,7 );

2. Выполняют моделирование технологического процесса изготовления деталей, аналогично п. 3.2. (2,3,4,5);

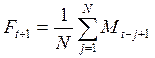3. В ячейках К9-К53 рассчитывают скользящее среднее для 5-и предыдущих значений отклонения величины скользящего среднего от величины уставки  по формуле , где ;

4. В ячейках L9-L53 рассчитывают знак скользящего среднего для 5-и предыдущих значений отклонения величины скользящего среднего от величины уставки

          ;

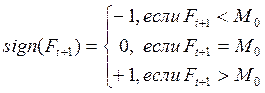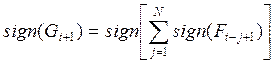5. В ячейках M14-M53 рассчитывают медиану - скользящее среднее для 5-и предыдущих значений знака -  по формуле , где ;

6. Величины «Ряда параметров» и округленной величины сравнения с уставкой (I4-I53) выводят на график 1;

7. Величины «Ряда параметров» и знака  отклонения величины скользящего среднего от величины уставки  (L9-L53) выводят на график 2;

8. Величины «Ряда параметров» и медианы (M14-M53) скользящего среднего -  выводят на график 3;

9.  На графиках 1, 2, 3 определяют номера деталей с которых следует произвести наладку;

10. Определяют текущие величины параметра  деталей (в массивах (I4-I53), (L9-L53), (M14-M53) ) с которых следует производить наладку;

11. Определяют количества годных деталей необработанных из-за раннего включения автоподналадки до устойчивого превышения допуска (упущенные возможности процесса.

12. Определяют количества бракованных деталей:

-  до включения автоподналадки;

-  до устойчивого превышения допуска в процессе обработки.

3.4. Учебные исследования процесса моделирования автоподналадки технологического оборудования

 Факторы влияющие на процесс:

1. Наклон тренда

2. Дисперсия процесса

3. Реализации случайного процесса

4. Положение уставки

5. Положение и ширина зоны подналадки

Оценки качества процесса подналадки:

1. Момент включения подналадки (номер детали).

2. Количество годных деталей необработанных в процессе до устойчивого превышения допуска (упущенные возможности процесса) , номер детали.

3. Количество бракованных деталей пропущенных при подналадке .

4. Статистические оценки (1, 2. 3) при вариации  факторов (параметров процесса) различных реализациях.

5. Количество ложных срабатываний подналадки.

Вероятности:

1. Вероятность не принятия решения о поднадладке при налаженном процессе  (истинное значение параметра в пределах допуска) – Р11.

2. Вероятность принятия решения о подналадке  при налаженном процессе истинное значение параметра в пределах допуска) (Ошибка 1-го рода) – Р12.

3. Вероятность  не принятия решения о подналадке при разладке процесса (истинное значение параметра за  пределами допуска) (Ошибка 2-го рода) - Р21.

4. Вероятность принятия решения о подналадке при разладке процесса (истинное значение параметра за пределами допуска)  – Р22.

4. Оформление отчета

Отчет должен содержать:

а) цель работы;

б) лист с отпечатанными последовательностями и результатами преобразования статистических данных по каждому методу реализации автоподналадки (один на бригаду студентов);

в) графики структуры суммарной погрешности для разных методов;

г) выводы.

5. Контрольные вопросы

5.1. Назовите и охарактеризуйте составляющие суммарной погрешности в случае дискретной обработки.

5.2. В чем сущность метода автоподналадки?

5.3. В чем сущность метода подналадки по одной детали?

5.4. Определение погрешности метода подналадки по одной детали.

5.5. Структура суммарной погрешности при подналадке.

5.6. Определение уставки для метода подналадки по одной детали.

5.7. В чем сущность метода подналадки по положению центра группирования?

5.8. Определение погрешности метода подналадки по положению центра группирования.

5.9. Определение уставки для метода подналадки  по положению центра группирования.

5. 10. Сравните между собой методы автоподналадки.

Литература

1. Технологическое обеспечение качества продукции в машиностроении/ Под ред. Г.Д. Бурду и С.С. Волосова. М. : Машиностроение. 1975.-280с.

2. Электрические методы автоматического контроля / Под ред. Б.К. Карандеева. М.: Энергия. 1965.-384с.

3. Лопухин В.А. Некоторые вопросы оптимизации автоматического контроля изделий/ Труды ЛИАП. Вып. 48. Л.: ЛИАП. 1966.-с.345-352.

4. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М., Гостехиздат. 1955.

5. Бусленко Н.П. Моделирование сложных систем. М., Наука. 1978. 399с.

6. Цветков А.Ф. Вероятностное моделирование: Учебное пособие. Рязань.: РРТИ. 1989. 64с.