ИМНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Высшая математика»
Курсовая работа
На тему: «Исследование надежности системы»
Выполнил студент
Группы ЭТ – 301
Стрельцов А.
Санкт – Петербург
2004
1. Исходная система.
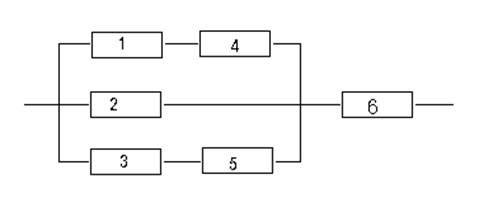
Представим эту схему, как соединение двух последовательных элементов.
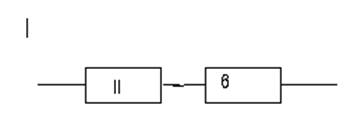
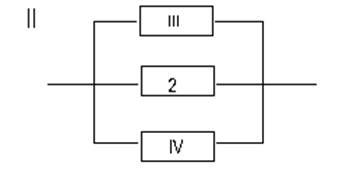
где II элемент это параллельное соединение 2-ого, III–его и IV-ого элементов, III элемент это последовательное соединение 1-ого и 4-ого элементов, а IV элемент это последовательное соединение 3-его и 5-ого элементов.
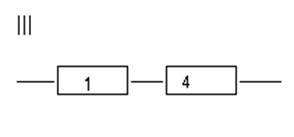
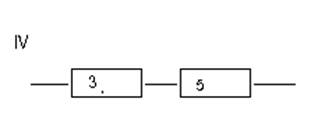
Отказ системы:
АI = AII*A6
AII = AIII+A2+AIV
AIII = A1*A4
AIV = A3*A5
Aобщ= ((A1*A4)+A2+(A3*A5))*A6
Робщ =
(1-(1-(1-A1)*(1-A4))*(1-A2)*(1-(1-A3)*(1-A5)))*(1-A6)
2. Таблица значений функций распределения
вероятности отказов схемы.
|
T |
Q |
P |
f |
|
0 |
0 |
1 |
0 |
|
80 |
0,001903364 |
0,998096636 |
2,37921E-05 |
|
160 |
0,002965339 |
0,997034661 |
1,32747E-05 |
|
240 |
0,005089685 |
0,994910315 |
2,65543E-05 |
|
320 |
0,008968577 |
0,991031423 |
4,84862E-05 |
|
400 |
0,01541922 |
0,98458078 |
8,0633E-05 |
|
480 |
0,02527023 |
0,97472977 |
0,000123138 |
|
560 |
0,03921252 |
0,96078748 |
0,000174279 |
|
640 |
0,05769523 |
0,94230477 |
0,000231034 |
|
720 |
0,08088923 |
0,91911077 |
0,000289925 |
|
800 |
0,1087044 |
0,8912956 |
0,00034769 |
|
880 |
0,1408367 |
0,8591633 |
0,000401654 |
|
960 |
0,1768251 |
0,8231749 |
0,000449855 |
|
1040 |
0,2161063 |
0,7838937 |
0,000491015 |
|
1120 |
0,2580611 |
0,7419389 |
0,000524435 |
|
1200 |
0,3020495 |
0,6979505 |
0,000549855 |
|
1280 |
0,3474376 |
0,6525624 |
0,000567351 |
|
1360 |
0,3936153 |
0,6063847 |
0,000577221 |
|
1440 |
0,440008 |
0,559992 |
0,000579909 |
|
1520 |
0,4860849 |
0,5139151 |
0,000575961 |
|
1600 |
0,5313638 |
0,4686362 |
0,000565986 |
|
1680 |
0,5754142 |
0,4245858 |
0,00055063 |
|
1760 |
0,6178595 |
0,3821405 |
0,000530566 |
|
1840 |
0,6583784 |
0,3416216 |
0,000506486 |
|
1920 |
0,6967057 |
0,3032943 |
0,000479091 |
|
2000 |
0,7326326 |
0,2673674 |
0,000449086 |
|
2080 |
0,7660063 |
0,2339937 |
0,000417171 |
|
2160 |
0,7967282 |
0,2032718 |
0,000384024 |
|
2240 |
0,8247521 |
0,1752479 |
0,000350299 |
|
2320 |
0,8500808 |
0,1499192 |
0,000316609 |
|
2400 |
0,8727617 |
0,1272383 |
0,000283511 |
|
2480 |
0,8928815 |
0,1071185 |
0,000251498 |
|
2560 |
0,9105604 |
0,0894396 |
0,000220986 |
|
2640 |
0,9259461 |
0,0740539 |
0,000192321 |
|
2720 |
0,9392064 |
0,0607936 |
0,000165754 |
|
2800 |
0,9505234 |
0,0494766 |
0,000141463 |
|
2880 |
0,9600865 |
0,0399135 |
0,000119539 |
|
2960 |
0,9680873 |
0,0319127 |
0,00010001 |
|
3040 |
0,9747137 |
0,0252863 |
8,283E-05 |
|
3120 |
0,9801465 |
0,0198535 |
6,791E-05 |
|
3200 |
0,9845553 |
0,0154447 |
5,511E-05 |
|
3280 |
0,9880966 |
0,0119034 |
4,42662E-05 |
|
3360 |
0,9909118 |
0,0090882 |
3,519E-05 |
|
3440 |
0,9931267 |
0,0068733 |
2,76863E-05 |
|
3520 |
0,9948512 |
0,0051488 |
2,15563E-05 |
|
3600 |
0,99618 |
0,00382 |
1,661E-05 |
|
3680 |
0,9971931 |
0,0028069 |
1,26638E-05 |
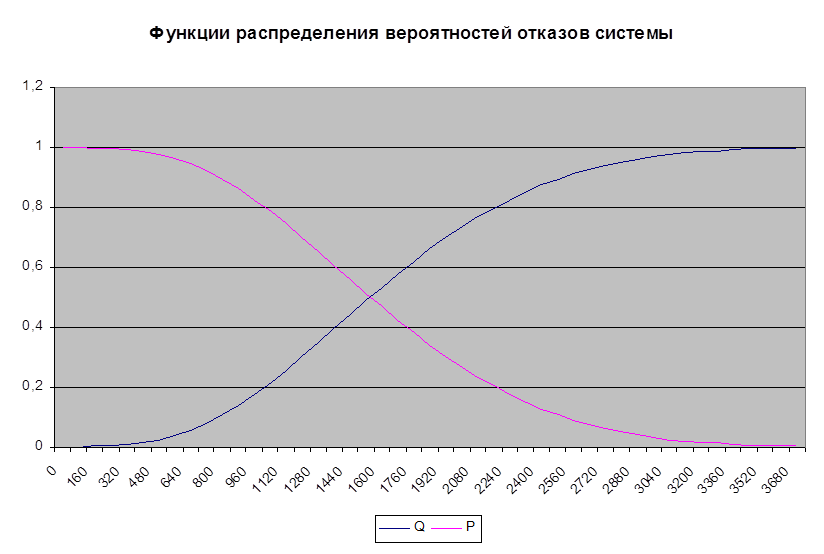
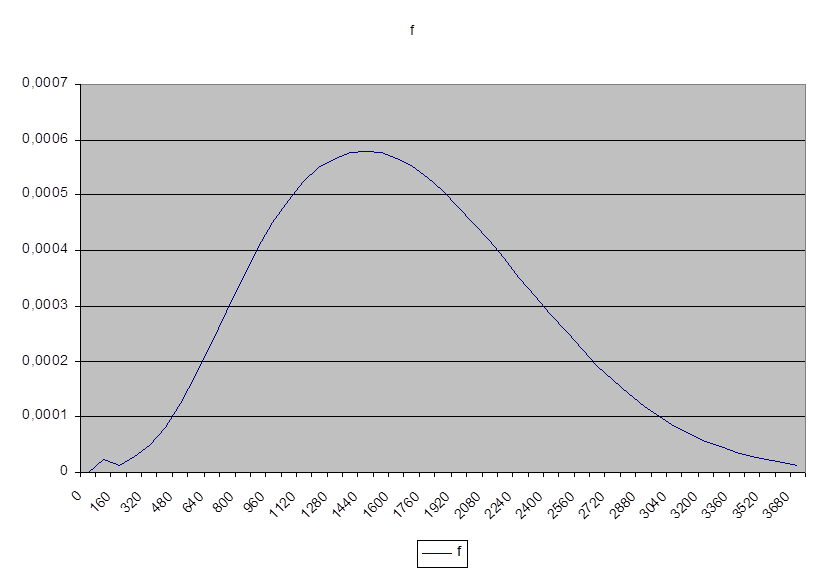
3. Математическое ожидание и дисперсия.
3.1. Математическое ожидание.
МТ = ò P(t) dt = (P0+Pn/2+(P1+P2+…+Pn-1))*∆t
MT = 1641,736356
3.2. Дисперсия.
DT = MT2 – (MT)2
(MT)2 = 2 ò t*P(t) dt = 2*∆t*(P1t1 +P2t2 +…+ Pntn)
(MT)2 = 3012865,812
DT = 3012865,812-(1641,736356)^2 = 317567.5494
s = Ö DT = 564
4. Вероятность без отказанной работы
Находим вероятность без отказанной работы системы в течении t1 ³ 400,
t2³ 800, t3³ 1600 по графикам функций Q(t) или P(t)
А) t1 ³ 400, вероятность без отказанной системы расчета равна:
P £ 0,98458078
Б) t2³ 800, вероятность без отказанной системы расчета равна:
P £0,8912956
В) t3³ 1600, вероятность без отказанной системы расчета равна:
P £0,4686362
5. Наработка системы до отказа.
5.1. Для схемы.
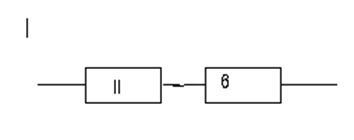
формула выглядит так: min (TII;T6)
II элемент
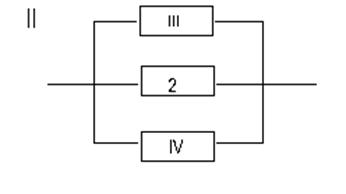
формула для этого элемента: max (TIII;T2’TIV)
III элемент
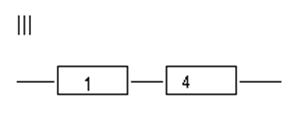
формула: min (T1;T4)
IV элемент
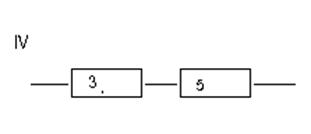
min (T3;T5)
Тогда общая формула вычисления наработки системы до отказа будет иметь вид:
Min (min (T1;T4); T2; min (T3;T5); T6)
5.1. Запишем в таблицу результат статического моделирования Т, по возрастающей:
|
352 |
996 |
1346 |
1943 |
2400 |
|
533 |
1057 |
1350 |
1950 |
2473 |
|
731 |
1123 |
1390 |
2063 |
2503 |
|
781 |
1143 |
1471 |
2088 |
2555 |
|
808 |
1160 |
1543 |
2145 |
2681 |
|
819 |
1189 |
1611 |
2246 |
2771 |
|
910 |
1246 |
1618 |
2248 |
2815 |
|
953 |
1300 |
1861 |
2291 |
2832 |
|
960 |
1317 |
1881 |
2312 |
3231 |
|
990 |
1339 |
1935 |
2332 |
3595 |
Интервал t € [352; 3595]
Число частичных интервалов N = [√n] = [√50] = 7
Min T = 352 = a
Max T = 3595 = b
Величина интервала h = (3595-352)/7 = 463
Составим таблицу распределения выборки.
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Границы интервала |
(352; 808] |
(808; 1246] |
(1246; 1618] |
(1618; 2145] |
(2145; 2555] |
(2555; 2832] |
(2832; 3595] |
|
Значение ti |
580 |
1027 |
1432 |
1881.5 |
2350 |
2693.5 |
3213.5 |
|
Эмпирические частоты, n |
5 |
12 |
10 |
8 |
9 |
4 |
2 |
|
эмпирические частоты, ni/n |
0.1 |
0.24 |
0.2 |
0.16 |
0.18 |
0.08 |
0.04 |
Построим гистограмму относительных частот:
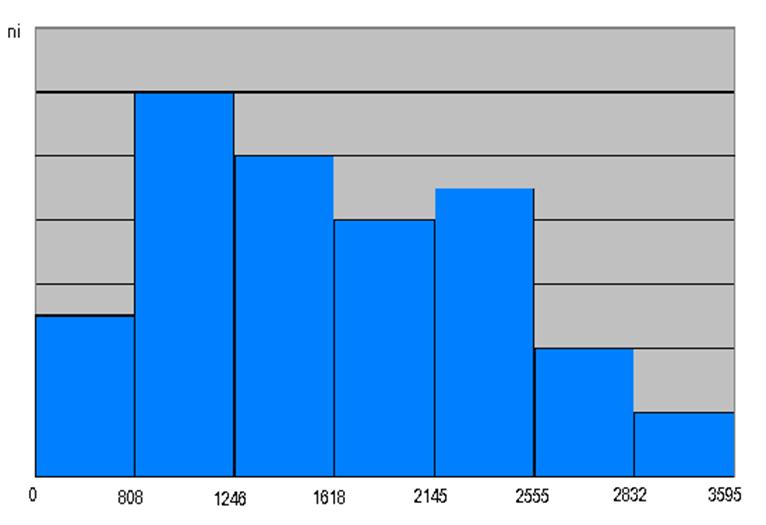
Найдем выборочное среднее:
t = (t1 + t2 + … + tn)/50 = n1/n*T1 + n2/n*T2 +… +n7/n*T7
t = 1658,94
Найдем выборочную дисперсию:
S2 = t2– (t)2= n1/n*T1^2 + n2/n*T2^2 +… +n7/n*T7^2 – (t)^2
S2 = 3250815,19 – (1658,94)^2 = 498733.2664
Выборочное средне квадратное отклонение равно:
S = ÖS^2 = 685
6. найдем доверительные интервалы для математического ожидания и составим таблицу:
|
g |
t |
x |
a1 |
a2 |
|
0,9 |
1,645 |
159.36 |
1499.31 |
1818.3 |
|
0,95 |
1,96 |
189.87 |
1469.07 |
1848.81 |
|
0,99 |
2,575 |
249.45 |
1409.49 |
1908.39 |
X = t*(S/Ön)
a1 = t - x
a2 = t + x
7. Проверим гипотезу Н0 о виде распределения вероятности отказа системы с помощью критерия х2 (Пирсона).
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Границы интервала |
(352; 808] |
(808; 1246] |
(1246; 1618] |
(1618; 2145] |
(2145; 2555] |
(2555; 2832] |
(2832; 3595] |
|
Эмпирические частоты, n |
5 |
12 |
10 |
8 |
9 |
4 |
2 |
|
теоретические частоты, npi |
5,02 |
10,8 |
10,66 |
12,48 |
5,92 |
2,24 |
2,1 |
n/pi = (Q(Tmax) – Q(Tmin))
x2 = S (ni - npi)2/npi = 4,772532662
Число степеней свободы l = 7-1 = 6
Критическая точка: х2 кр (0.1;6) = 10.6
х2 кр (0.05;6) = 12.6
х2 кр (0.01;6) = 16.8
Для рассматриваемых уравнений зависимости х2< х2 кр. Оснований опровергнуть гипотезу Н0, нет. Эта гипотеза состоит в том, что полученная функция распределена в результате статистического моделирования, может описать функцию распределения, данную в текущей работе. В пределах погрешностей они должны совпасть.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.