Моделирование потоков систем массового обслуживания с заданным законом распределения

ОАО РЖД

Петербургский Государственный Университет Путей Сообщения

Кафедра

«Прикладная математика»

Задание

«Моделирование потоков систем массового обслуживания

с заданным законом распределения»

Выполнил студент

группы ЭТ–302

Туцкий А.И.

Проверила: доцент Вашакидзе Л.С.

Санкт-Петербург

2006

1.Моделирование непрерывных случайных величин.

(закон распределения Эрланга k=3,=4)

1. Теоретическая часть:

        Стандартный способ моделирования случайной величины ξ основан на том известном факте, что случайная величина η=F_ξ (ξ) имеет равномерное распределение на промежутке (0,1). Таким образом, для получения выборки объёма N из распределения F_ξ нужно получить N значений случайной величины, имеющей равномерное на промежутке (0,1) распределение, и обратить уравнение

α = F_ξ (ξ),

т.е. по каждому значению α как бы «восстановить» соответствующее значение случайной величины ξ, получив тем самым моделирующую формулу

x= F_ξ^-1(α),

где F_ξ^-1 – функция, обратная F_ξ. Наиболее удобен этот способ для моделирования таких распределений, у которых F_ξ монотонно возрастает, а F_ξ^-1 может быть вписана явно в форме, не требующей сложных вычислений.

        Приведём пример моделирующей формулы для распределения Эрланга с параметрами k=3,=4 и плотностью:

 

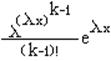                          , x > 0    

f(X)=

0                            , x <= 0

График:

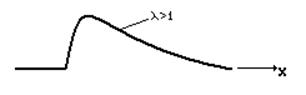
Моделирующая формула или прием:

=

имеют показательное распределение с параметром .

Основные численные характеристики:

Е

D

Для ряда  модельных распределений существуют специальные приёмы моделирования, применяемые для задания последовательностей значений случайной величины в тех случаях, когда получение моделирующих формул затруднено или невозможно; иногда используются в качестве альтернативы.

2.Текст программы:

l=4;

X1=-log(1-rand(1,200))/l;

X2=-log(1-rand(1,200))/l;

X3=-log(1-rand(1,200))/l;

X=X1+X2+X3;

hist(X)

m=mean(X)

m =0.7515

s1=std(X);

s2=s1^2

s2 =0.1727

x=0:0.1:10;

y=4*(4*x).^2/2.*exp(-4*x);

figure(1);plot(x,y,'r','LineWidth',3);grid

3.Гистограмма и график распределения непрерывной случайной величины:

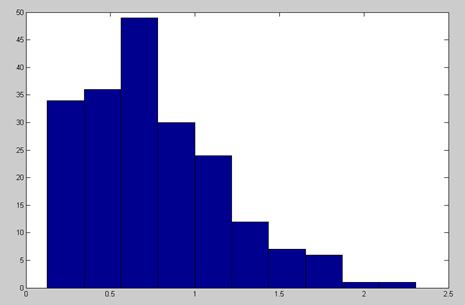
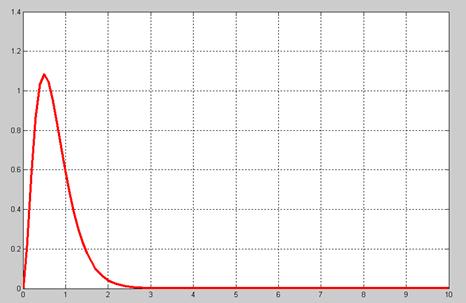
Вывод:

В данной лабораторной работе мы исследовали распределение Релея. В ходе проделанной работы мы получили выборку, сделали элементарную статистическую обработку, построили график функции плотности (гистограмму относительных частот) и построили график теоретической плотности функции. В результате практических исследований мы получили подтверждение теоретическим сведениям.

2.Моделирование дискретных случайных величин

(закон распределения Пуассона λ=1)

1. Теоретическая часть:

Условно случайные величины можно разделить на 2-а типа:

1)  дискретные случайные величины

2)  непрерывные случайные величины

Дискретные случайные величины – это случайные величины, множество которых конечно или счётно.

Параметры распределения – это математическое ожидание и дисперсия значений случайной величин.

Пример параметров распределения для распределения Пуассона:

МХ=λ  DX=λ

     В задачах моделирования случайных величин во всех системах программирования базовой является функция которая называется «датчик случайных чисел» – rand в MATLAB.

        Для того чтобы вычислить вероятности значений случайной величины используя аналитическую форму их задания можно для каждого из законов построить соответствующие реккурентные соотношения.

        Целью обработки является доказательство с помощью статистических оценок, что моделируемая случайная величина является заданной.

2.Текст программы:

Моделирование распределения Пуассона с параметром λ =1

l=1

N=100

P0=exp(-1);

R=l/( l+1);

for J=1:N,

ALF=rand;

Y=ALF;

P=P0;

l=0;

Y=Y-P;

while Y>0,

P=P*eval(R);

l=l+1;

Y=Y-P;

end;

REZ=X(1:10);

for k=l:N/10-1,

REZ=[REZ;X(10*k+1,10*(k+1))];

end;

REZ

2)  Выборка:

l=1

N=100

REZ= 1  0  0  0  1  1  0  0  1  2

 3  0  0  2  0  1  3  1  2  0

0  2  1  2  1  1  0  0  0  0

1  2  1  2  1  1  1  1  2  0

0  0  1  1  4  1  1  0  1  1

1  0  1  2  2  3  2  0  1  1

0  2  1  1  0  1  3  0  1  1

1  1  1  1  1  2  1  1  1  1

1  1  2  1  0  1  4  2  1  1

0  1  0  0  1  2  1  6  3  0

Элементарная статистическая обработка:

X	0	1	2	3	4	6
P	0.3679	0.3679	0.1840	0.0613	0.153	0.0005
nк	28	48	16	5	2	1
P= nк/N	0.28	0.48	0.16	0.05	0.02	0.01

P(K=X)= (λ^k/K!)*e ^–λ

X= 1/N*ΣX_i=1/100*109=1.09

MX=λ=1 DX=λ=1

s²=(1/(N-1))*( ΣX_i²-(X)²)= (1/(100-1))*( 109²-1.09²)=1.08

Вывод: изучая 2 и 4 строки таблицы можно сделать вывод о том, что задача решена правильно т.к. численные значения приблизительно сходятся.