Анализ марковских СМО. Компьютерное моделирование и расчет показателей СеМО

МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра: «Прикладная математика»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К курсовой работе

“Анализ марковских СМО. Компьютерное моделирование и расчет показателей СеМО”

Выполнил студент                                           Петров А.В.

Группа                                                             ЭС – 205 Преподаватель                                                Грибкова Н. В.

САНКТ-ПЕТЕРБУРГ

2003

Содержание.

1.  Анализ марковских СМО.

1.1.    Условие задачи.

1.2.   Кодировка Кендалла.

1.3.   Теоретическая часть.

      1.3.1.  Структура СМО

      1.3.2. Марковские системы обслуживания.

     1.4.    Компьютерное моделирование марковских систем.

       1.4.1.   Текст программы.

        1.4.2.   Результаты.

        1.4.3.   Состояния процесса Q(t) в моменты изменений состояния системы.

   1.5.В     Вычисление числовых характеристик открытых марковских СМО.

          1.5.1.    Текст программы.

                 1.5.2.   Результаты.

                 1.5.3.   График функции распределения времени ожидания FW(t).

      1.6.     Сравнение результатов.

    2.  Компьютерное моделирование и расчет показателей             СеМО.

       2.1.   Условие задачи.

         2.2.    Кодировка Кендалла.

   2.3.    Составление схемы.

         2.4.   Теоретическая часть.

          2.4.1.  Определение СеМО.

      2.4.2. Матрица маршрутизации.

         2.5.     Решение уравнения баланса.

           2.5.1. Нахождение полных интенсивностей потоков входящих в узлы 1-4

           2.5.2. Решение уравнений с помощью системы MatLab

         2.6.  Расчёт вероятности состояний и характеристики работы узлов входящих в сеть, с использованием системы Маthlab.

      2.6.1.   Текст программы.

        2.6.2.   Результаты.

        2.6.3.   Состояния процесса для каждого из узлов.

   2.7.   Программа, выполняющая имитационное моделирование работы в сети.

           2.7.1.    Текст программы.

                  2.7.2.   Результаты.

      2.8.    Сравнение результатов.

    3.    Вывод.

    4.    Библиографический список.

1.  Анализ марковских СМО.

1.1  Условие задачи.

     В отдел агентства фирменного транспортного обслуживания, в котором работают два сотрудника, поступает поток клиентов с заявками на перевозки. Интервалы времени между поступлениями клиентов – независимо одинаково распределённые случайные величины, имеющие показательный закон распределения с параметром λ=6 клиентов/час. Время обслуживания одного клиента имеет показательный закон распределения со средним значением 10 минут. Число мест для ожидания клиентов не ограничено.

1.2  Кодировка Кендалла.

Для данной системы кодировка Кендалла имеет следующий вид: М|М|2|∞.

1.3  Теоретическая часть.

             Сетью массового обслуживания (СеМО) называют совокупность одновременно и            взаимосвязанных работающих систем массового обслуживания (СМО).

      1.3.1.    Структура СМО:

       Математическая модель СМО составляет четыре основных элемента:

a)  Входящий поток требований;

b)  Время обслуживания каждого требования;

c)  Число обслуживающих устройств;

d)  Алгоритм обслуживания.

       Первый и второй элементы определяют случайную часть СМО, третий и четвертый – способ организации. Заданием этих элементов порождается многообразие систем обслуживания.

1.3.2.   Марковские системы обслуживания.

        Сеть массового обслуживания составляют СМО, которые являются компонентами СеМО. Многие задачи, связанные с определением характеристик работы сетей, сводятся к нахождению характеристик составляющих ее узлов (СМО).

1.4.  Компьютерное моделирование марковских систем.

 1.4.1.   Текст программы.

      % Ввод исходных данных

lambda=input(' введите lambda');

mu=input('введите mu');

m=input('введите m');

% Определение вспомогательных переменных

Num=input('число изменений состоаний системы за врема моделированиа ');

s=1;% индекс текущего состоаниа системы

T=zeros(1,Num);% вектор моментов изменениа состоаний

Qt=zeros(1,Num);% состоаниа процесса Q(t) в моменты изменений состоаниа системы

Time=zeros(1,Num);% вектор, в котором накапливаютса суммарные времена пребываниа

%системы в состоаниах 0,1,...,Num

for i=2:Num

    if Qt(i-1)==0

        v=Inf;

        u=-log(rand)/lambda;

    else

        u=-log(rand)/lambda;

        qs=min(m,Qt(i-1));% число работающих приборов

        v=-log(rand)/(qs*mu);

    end;

    delta_time=min(u,v);

    T(i)=T(i-1)+delta_time;

    Time(s)=Time(s)+delta_time;

    if u<v

        Qt(i)=Qt(i-1)+1;

    else

        Qt(i)=Qt(i-1)-1;

    end;

        s=Qt(i)+1;% индекс текущего состоаниа

    end;

    z=zeros(1,Num);

    mvect=ones(1,Num)*m;

    qt=max(z,Qt-mvect);% очередь за врема моделированиа

    % Построение на одном экране графика состоаний системы и числа клиентов

    % в очереди

    subplot(211);

    plot(T,Qt);

    subplot(212);

    plot(T,qt);

    disp('оценки системы с ожиданием');

    disp('полученные на основе моделированиа');

    Psost=Time/T(Num);

    disp('вероатность простоа');

    N=input('количество вероатностей, которые нужно вывести на экран ');

    disp('вероатности состоаний 1..n');

    disp(Psost(2:N+1));

    disp('вероатность ожиданиа');

    Pw=1-sum(Psost(1:m));

    disp(Pw);

    disp('среднее число заавок в системе');

    k=0:(Num-1);

    Qsr=k*Psost';

    disp(Qsr);

    disp('среднее число заавок в очереди');

    qsr=max(z,k-m)*Psost';

    disp(qsr);

1.4.2  Результаты.

      введите lambda 10

введите mu 6

введите m 2

число изменений состоаний системы за врема моделированиа 100

количество вероатностей, которые нужно вывести на экран 10

  Columns 1 through 5

    0.2797    0.1922    0.2654    0.1020         0

  Columns 6 through 10

         0         0         0         0         0

вероатность ожиданиа

    0.5596

среднее число заавок в системе

    1.8683

среднее число заавок в очереди

    0.4694

 1.4.3.   Состояния процесса Q(t) в моменты изменений состояния системы.

 

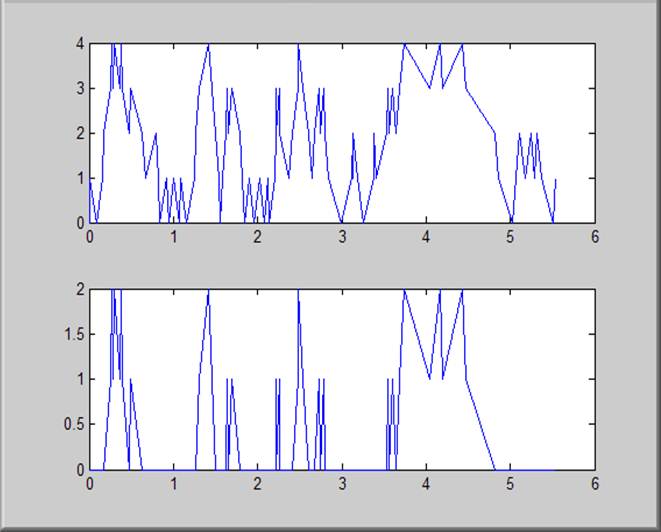
1.5.  Вычисление числовых характеристик открытых марковских СМО.

1.5.1.    Текст программы.

 % Ввод исходных данных

lambda=input('введите lambda');

mu=input('введите mu');

m=input('введите m');

rho=lambda/mu;

rho_m=rho/m;