Математика \ Прикладная математика

Анализ марковских СМО. Компьютерное моделирование и расчет показателей СеМО, страница 3

M=200;

M1=M+1;

TIME=zeros(N,M1);

P_cumsum=(cumsum(Pr'))';

for i=2:Num

for j=1:N

if gamma(j)==0

U(j)=Inf

else

U(j)=-log(rand)/gamma(j);

end;

if Q(j,i-1)==0

V(j)=Inf;

else

end

end;

U_min=min(U);

V_min=min(V);

delta_time=min(U_min,V_min);

T(i)=T(i-1)+delta_time;

for j=1:N

if l(j)<=M1

TIME(j,l(j))=TIME(j,l(j))+delta_time;

end;

if U_min<V_min

k=find(U==U_min);

Q(k,i)=Q(k,i-1)+1;

l(k)=Q(k,i)+1;

else

k=find(V==V_min);

Q(k,i)=Q(k,i-1)-1;

l(k)=Q(k,i)+1;

j=min(find(P_cumsum(k,:)-rand>0));

if j<=N

Q(j,i)=Q(j,i)+1;

l(j)=Q(j,i)+1;

end

end;

Psost=TIME/T(Num);

for j=1:N

plot(T,Q(j,:),T,q(j,:));

pause;

end;

Qsr=zeros(1,N);

P0=zeros(1,N);

z=zeros(1,M1);

k=0:M;

for j=1:N

disp('Характеристики');disp(j);disp('-го узла');

P0(j)=Psost(j,1);

disp('P0=');

disp(P0);

disp('Среднее число заавок');

Qsr(j)=k*(Psost(j,:))';

disp(Qsr);

end

disp('Среднее число заавок в сети');

Qsr_netw=sum(Qsr);

disp(Qsr_netw);

disp('Среднее врема задержки в сети');

Tof_stay_netw=Qsr_netw/sum(gamma);

disp(Tof_stay_netw);

2.6.2 Результаты.

Характеристики

1-го узла

P0=

1.0e-003 *

0.6309 0 0 0

Среднее число заавок

1.1155 0 0 0

Характеристики

2-го узла

P0=

1.0e-003 *

0.6309 0.9221 0 0

Среднее число заавок

1.1155 1.3399 0 0

Характеристики

3-го узла

P0=

1.0e-003 *

0.6309 0.9221 0.8706 0

Среднее число заавок

1.1155 1.3399 1.2476 0

Характеристики

4-го узла

P0=

1.0e-003 *

0.6309 0.9221 0.8706 0.7124

Среднее число заавок

1.1155 1.3399 1.2476 1.9484

Среднее число заавок в сети

5.6514

Среднее врема задержки в сети

0.7064

2.6.3. Состояния процесса для каждого из узлов.

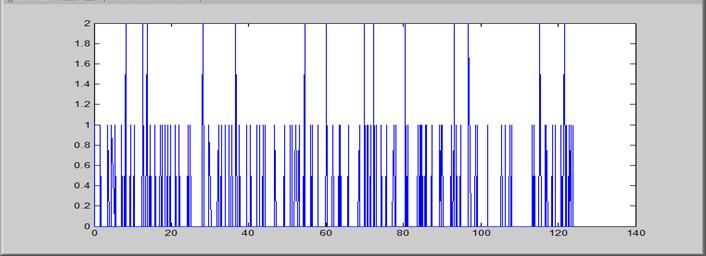
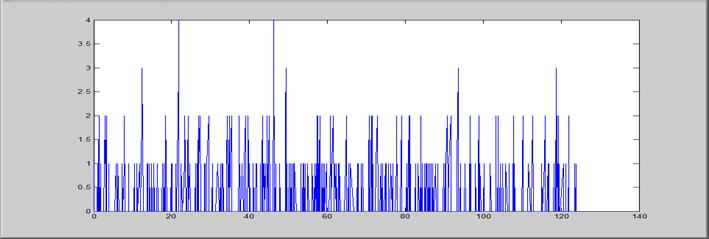
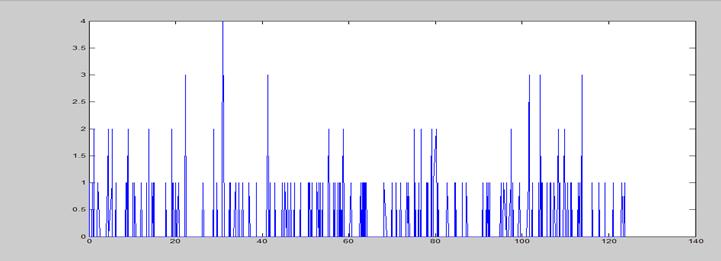
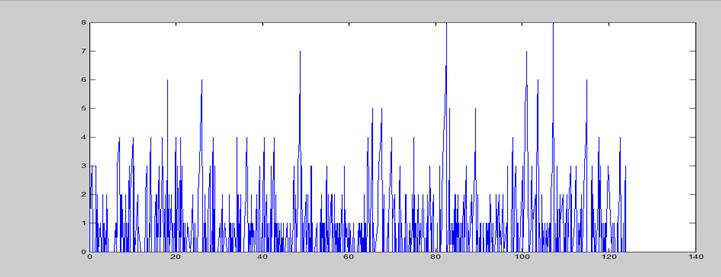
2.7. Программа, выполняющая имитационное моделирование работы в сети.

2.7.1. Текст программы.

mu=[2 4 1 3];

gamma=[1 2 1 4];

N=4;

P=[0 1/2 0 0;0 0 1/2 0;0 0 0 1/2;1/2 0 0 0;];

disp('Расчёт показателей открытой сети Джексона');

E=eye(N,N);

% Решение системы уравнениа баланса

lambda=gamma/(E-P);

ro=lambda./mu;

% Расчёт характеристик

for i=1:N

K=input('Сколько вероатностей вычислать');

% Вычисление вероатностей Р0,Р1,...,Р(к-1)

x=1:K-1;

slave1=ones(1,K-1)*ro(i);

slave2=slave1./x;% вектор длины К-1, равный (р,р/2,...,р/(к-1))

slave=cumprod(slave2);% вектор (р,р/(2!),...,р/(К-1)!)

disp('Вероатность простоа');

P0(i)=exp(-ro(i));

disp(P0);

disp('Вероатности состоаний 1,...,К-1');

Psost=slave*P0(i);

disp(Psost);

disp('Характеристики');

disp(i);

disp('-го узла');

disp( 'Вероатность ожиданиа');

disp(P0(i));% вероатность простоа

disp('Psost');% вероатности первых К состоаний

disp(Psost);

disp('Среднее число заавок');

Qsr(i)=ro(i);

disp(Qsr(i));

disp('Среднее врема пребываниа в узле');

Tsr(i)=1/mu(i);

disp(Tsr(i));

end;

disp('Сетевые характеристики');

disp('Среднее число заавок в сети');

Qsr_netw=sum(Qsr);

disp('Qsr_netw=');

disp(Qsr_netw);

gamma=sum(gamma);

disp('Cреднее врема задержки в сети');

T=Qsr_netw/gamma;

disp('T=');

disp(T);

end

2.7.2 Результаты.

Расчёт показателей открытой сети Джексона

Сколько вероатностей вычислать 10

Вероатность простоа

0.1546 0.3803 0.0532 0.1617

Вероатности состоаний 1,...,К-1

0.2887 0.2694 0.1676 0.0782 0.0292 0.0091 0.0024 0.0006 0.0001

Характеристики

1-го узла

Вероатность ожиданиа

0.1546

Psost

0.2887 0.2694 0.1676 0.0782 0.0292 0.0091 0.0024 0.0006 0.0001

Среднее число заавок

1.8667

Среднее врема пребываниа в узле

0.5000

Сколько вероатностей вычислать 10

Вероатность простоа

0.1546 0.3803 0.0532 0.1617

Вероатности состоаний 1,...,К-1

0.3677 0.1777 0.0573 0.0138 0.0027 0.0004 0.0001 0.0000 0.0000

Характеристики

2-го узла

Вероатность ожиданиа

0.3803

Psost

0.3677 0.1777 0.0573 0.0138 0.0027 0.0004 0.0001 0.0000 0.0000

Среднее число заавок

0.9667

Среднее врема пребываниа в узле

0.2500

Сколько вероатностей вычислать 10

Вероатность простоа

0.1546 0.3803 0.0532 0.1617

Вероатности состоаний 1,...,К-1

0.1561 0.2290 0.2239 0.1642 0.0963 0.0471 0.0197 0.0072 0.0024

Характеристики

3-го узла

Вероатность ожиданиа

0.0532

Psost

0.1561 0.2290 0.2239 0.1642 0.0963 0.0471 0.0197 0.0072 0.0024

Среднее число заавок

2.9333

Среднее врема пребываниа в узле

Сколько вероатностей вычислать 10

Вероатность простоа

0.1546 0.3803 0.0532 0.1617

Вероатности состоаний 1,...,К-1

0.2946 0.2684 0.1630 0.0743 0.0271 0.0082 0.0021 0.0005 0.0001

Характеристики

4-го узла

Вероатность ожиданиа

0.1617

Psost

0.2946 0.2684 0.1630 0.0743 0.0271 0.0082 0.0021 0.0005 0.0001

Среднее число заавок

1.8222

Среднее врема пребываниа в узле

0.3333

Сетевые характеристики

Среднее число заавок в сети

Qsr_netw= 7.5889

Cреднее врема задержки в сети

T= 0.9486

2.8 Сравнение результатов.

Параметры сети	Имитационный расчёт	Аналитический расчёт
Среднее число пассажиров на каждой станции	1.8222	5.6514
Среднее время задержки в сети	0.9486	0.7064

3. Вывод.

В данном курсовом проекте были рассмотрены марковские сети различных типов. Определены основные сетевые характеристики, построены графики основных процессов. Данные полученные аналитическим и имитационным способами моделирования различаются, но близки по значению.

4. Библиографический список.

Ю.В. Боровских, Н.В. Грибкова : «Системы и сети с очередями».

Методические указания: «Системы и сети с очередями в Mathlab».

Методические указания: «Марковские системы с очередями».

1 2 3

Скачать файл