% Проверка условиа существованиа стационарного режима
if rho_m>=1,
disp('стационарного режима не существует');
else
disp('стационарный режим существует');
K=input('сколько веротностей вычислить');
while K<=m
disp('K должно быть не меньше m+1');
K=input('сколько веротностей вычислить');
end;
% Вычисление вероатностей P0,P1,...,P(k-1)
x=1:m;
x1=ones(1,K-1-m)*m;
xx=[x,x1];% вектор длины К-1, равный (1,2,...,m,...,m)
slave1=ones(1,K-1)*rho;
slave2=slave1./xx;% вектор длины К-1, равный (p,p/2,...,p/m,...,p/m)
slave=cumprod(slave2);% вектор (p,p/(2!),...,p/(m!),...,p/(m!m )
disp('вероатность простоа');
P0=1/(1+sum(slave(1:m-1))+slave(m)/(1-rho_m));
disp(P0);
disp('вероатности состоаний 1,...K-1');
Psost=slave*P0;
disp(Psost);
disp('вероатность ожиданиа перед обслуживанием');
Pw=Psost(m)/(1-rho_m);
disp(Pw);
disp('вероатность обслуживаниа без ожидани');
Pww=1-Pw;
disp(Pww);
disp('Среднее число заавок в системе');
k=1:m-1;
Qsr=k*(Psost(1:m-1))'+m*Pw+Psost(m)*rho_m/(1-rho_m)^2;
disp(Qsr);
disp('среднее число заавок в очереди');
qsr=Psost(m)*rho_m/(1-rho_m)^2;
disp(qsr);
disp('среднее число занатых приборов');
qs=Qsr-qsr;
disp(qs);
disp('среднее врема ожиданиа');
W=qsr/lambda;
disp(W);
disp('среднее врема пребываниа в системе');
T=Qsr/lambda;
disp(T);
% График функции распределениа времени ожиданиа FW(t)
t=0:0.01:10;
FW=1-Pw*exp(-(m*mu-lambda)*t);
plot(t,FW);
end;
1.5.2. Результаты.
введите lambda 10
введите mu 6
введите m 2
стационарный режим существует
сколько веротностей вычислить 10
вероатность простоа
0.0909
вероатности состоаний 1,...K-1
0.1515 0.1263 0.1052 0.0877 0.0731 0.0609 0.0507 0.0423 0.0352
вероатность ожиданиа перед обслуживанием
0.7576
вероатность обслуживаниа без ожидани
0.2424
Среднее число заавок в системе
5.4545
среднее число заавок в очереди
3.7879
среднее число занатых приборов
1.6667
среднее врема ожиданиа
0.3788
среднее врема пребываниа в системе
0.5455
1.5.3. График функции распределения времени ожидания FW(t).
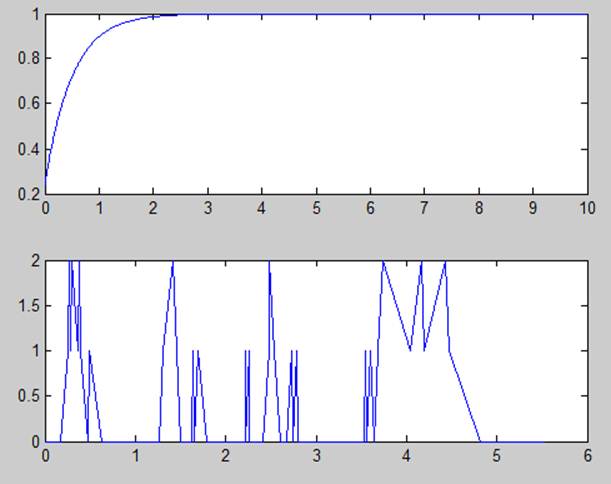
1.6. Сравнение результатов.
|
Параметры сети |
Имитационный расчёт |
Аналитический расчёт |
|
Вероятность ожидания |
0.5596 |
0.7576 |
|
Среднее число заявок в системе |
1.8683 |
5.4545 |
|
Среднее число заявок в очереди. |
0.4694 |
3.7879 |
2. Компьютерное моделирование и расчет показателей СеМО.
2.1 Условие задачи.
Сеть метрополитена состоит из станций (узлов). На каждую станцию извне поступает простейший поток пассажиров с интенсивностями γ=(1,2,1,4), причём каждая станция обслуживает пассажиров в режиме М|M|∞. Так что данный метрополитен представляет собой открытую СЕМО типа [M|M|∞]4. Предположим, что расширенная матрица маршрутизации имеет вид:
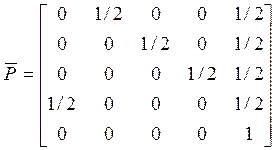 .
.
Интенсивность пребывания пассажира в сети равна µ=(2,4,1,3). В стационарном режиме определить:
1) решение уравнения баланса;
2) распределения числа пассажиров по станциям;
3) среднее число пассажиров на каждой станции.
2.2 Кодировка Кендалла.
Для данной системы кодировка Кендалла имеет следующий вид: [М|М|∞]4.
2.3 Составление схемы.
 |
2.4 Теоретическая часть.
2.4.1. Определение СеМО:
Сеть массового обслуживания
полностью задана, если каждый её узел определен как СМО и указана матрица ![]() .
.
Если все N
узлов сети одного типа, то будем обозначать её следующим образом: запись узла
сети в символике Кендалла будем возводить в степень N. Например,
![]() , m=(m1,
…, mN), -
условное обозначение СеМО, в которой на первый узел извне поступает простейший
поток требований, i-тый узел
содержит mi однотипных
обслуживающих приборов. Поступившее требование начинает обслуживаться на любом
свободном приборе. Время обслуживания распределено по показательному закону.
Если все приборы заняты, то требование становится в очередь i-того
узла и ожидает начала обслуживания.
Ограничения на длину очереди нет. После обслуживания в i-том
узле требование с вероятностью
, m=(m1,
…, mN), -
условное обозначение СеМО, в которой на первый узел извне поступает простейший
поток требований, i-тый узел
содержит mi однотипных
обслуживающих приборов. Поступившее требование начинает обслуживаться на любом
свободном приборе. Время обслуживания распределено по показательному закону.
Если все приборы заняты, то требование становится в очередь i-того
узла и ожидает начала обслуживания.
Ограничения на длину очереди нет. После обслуживания в i-том
узле требование с вероятностью ![]() мгновенно поступает на обслуживание
в j-й узел и с
вероятностью
мгновенно поступает на обслуживание
в j-й узел и с
вероятностью 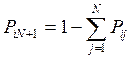 покидает сеть.
покидает сеть.
Свойства СеМО напрямую зависят от
структуры матрицы ![]() . Согласно типу матрицы
. Согласно типу матрицы ![]() введем понятие замкнутой, открытой и
смешанной СеМО.
введем понятие замкнутой, открытой и
смешанной СеМО.
СеМО называют замкнутой, если ![]() и отсутствуют потоки извне. В
противном случае СеМО называют разомкнутой.
и отсутствуют потоки извне. В
противном случае СеМО называют разомкнутой.
Разомкнутую сеть называют открытой, если все требования могут поступать в сеть и покидать её. Если же некоторая часть требований постоянно находится в сети, то такая СеМО называется смешанной.
Матрица ![]() соответствует
цепи Маркова с дискретным временем и множеством состояний {1,2, …, N,
N+1}.
соответствует
цепи Маркова с дискретным временем и множеством состояний {1,2, …, N,
N+1}.
2.4.2. Матрица маршрутизации.
Системы обслуживания, которые образуют сеть, называются узлами
этой СеМО. Занумеруем узлы СеМО числами 1, 2, …, N,
где N – число узлов сети. Предположим, что
требование, обслуживание которого закончилось в узле с номером i, с вероятностью pij
поступает на обслуживание в узел с номером j и с
вероятностью piN+1 покидает
сеть. Эти вероятности удовлетворяют условиям 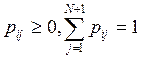 ,
i=1, …, N.
,
i=1, …, N.
Квадратная матрица ![]() называется
матрицей маршрутизации, а матрица
называется
матрицей маршрутизации, а матрица
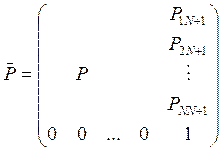
-расширенной матрицей маршрутизацией.
2.5. Решение уравнения баланса.
2.5.1 Нахождение полных интенсивностей потоков входящих в узлы 1-4:
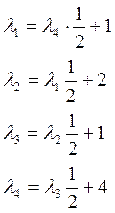
2.5.2. Решение уравнений с помощью системы MatLab:
Текст программы:
ga=[1,2,1,4]
E=eye(4,4);
P=[0 1/2 0 0;0 0 1/2 0;0 0 0 1/2;1/2 0 0 0];
la=ga/(E-P)
Результат выполнения программы:
la = 3,7333 3.8667 2,9334 5,4667
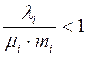
Следовательно возьмем ![]() равные:
равные:
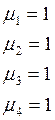
2.6. Расчёт вероятности состояний и характеристики работы узлов входящих в сеть, с использованием системы Маthlab.
2.6.1. Текст программы.
Num=1000;
gamma=[1 2 1 4];
mu=[2 4 1 3];
N=4;
Pr=[0 1/2 0 0;0 0 1/2 0;0 0 0 1/2;1/2 0 0 0];
T=zeros(1,Num);% Вектор моментов изменений состоаний
Q=zeros(N,Num);% Матрица состоаний узлов в моменты изменений состоаний сети
l=ones(1,N);% Номера состоаний узлов на текущий момент
U=zeros(1,N);
V=zeros(1,N);% Времена окончаний обслуживаниа в узлах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.