Основы молекулярной физики и термодинамики: Методические указания к практическим занятиям по курсу общей физики, страница 6

Задача 15. Идеальный двухатомный газ, содержащий количество вещества n = 1 моль и находящийся под давлением    Р₁ = 0,1 МПа при температуре Т₁ = 300 К,  нагревают при постоянном  объеме до давления Р₂ = 0,2 МПа. После этого газ изотермически  расширялся до начального давления и затем изобарно был сжат до начального объема V₁. Построить график цикла. Определить температуру Т газа для характерных точек цикла и его термический КПД h.

Дано: Р1= 0,1 Мпа = 1·105 Па Т1= 300 К Р2= 0,2 Мпа = 2·105 Па	Решение: В координатах Р, V график цикла имеет следующий вид
T2 –  ? Т3 –  ? h –  ?	V1             V2      V

Переход газа на участке 1-2 происходит изохорически при V₁ = const. Давления и температуры газов в состояниях 1 и 2 связаны между собой соотношением:                                                      

 =.

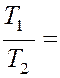
Отсюда T₂ = 2Т₁ = 600 K.

Так как переход газа  2-3 изотермический, то Т₂ = Т₃.

Термический КПД цикла определяется выражением

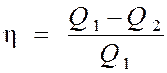,                                   (1)

где Q₁ –  количество теплоты, полученное от нагревателя за цикл,      Q₂ –  количество теплоты, отданное холодильнику за цикл.

Газ получает количество теплоты на участках 1-2 и 2-3

Q ₁= Q _1-2 + Q _2-3, где Q _1-2 = C _v v (T ₂ - T ₁) –  количество теплоты, полученное при изохорическом нагревании,

 –  количество теплоты, полученное при изотермическом расширении.

Газ отдает количество теплоты на участке 3-1 при изобарическом сжатии:

Q _3-1 = Q ₂ = C_р  

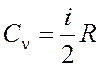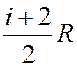–  молярная теплоемкость газа при V = const,                           C _р   –  молярная теплоемкость газа при P = const.

Подставив значения Q ₁ и Q ₂, С _v и С _рв формулу (1) получим:

,                      

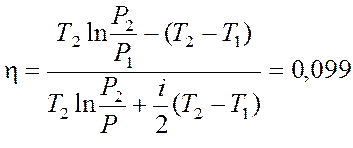Ответ: T ₂ = T ₃ = 600 K,    η = 9,9 %.

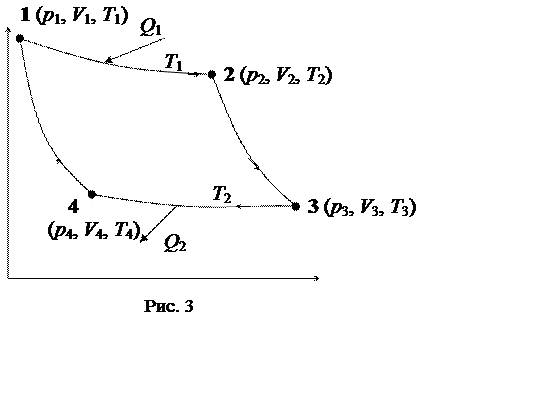
Задача16. Кислород массой 1 кг совершает цикл Карно. При изотермическом расширении газа его объём увеличивается в 2 раза, а при последующем адиабатическом расширении совершается работа 3000 Дж. Определить работу, совершенную за цикл.

Дано: V2 = 2V1 A2-3 = 3000 Дж i = 5	Решение: Идеальный цикл Карно состоит из двух изотерм и двух адиабат (рис. 3).
А - ?

На рисунке 3 участок 1-2 соответствует изотермическому расширению газа (Т₁ = Т₂), участок 2-3 – адиабатическому расширению газа, участок 3-4 – изотермическому сжатию (Т₃ = Т₄) и участок 4-1 – адиабатическому сжатию.

При изотермическом расширении внутренняя энергия идеального газа остается постоянной, следовательно, все подводимое тепло Q₁ идет на работу по расширению газа на участке 1-2, т.е.

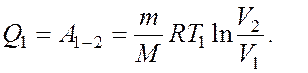                                                 (1)

При изотермическом сжатии на участке 3-4 Q₂ тепло отдается холодильнику (Q₂), и это количество теплоты определяется работой, затраченной на сжатие газа:

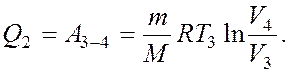                               (2)

Состояния 2 и 3 лежат на одной адиабате, поэтому можно записать:

                                       (3)

Для состояний 4 и 1, которые отвечают одной адиабате, имеем:

                                        (4)

Поделив выражение (3) на (4), получим:

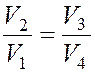,                                                   (5)

так как Т₁ = Т₂ и Т₃ = Т₄.

Работа при адиабатическом расширении на участке 2-3 равна:

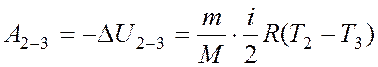                  (6)

Работа при адиабатическом сжатии на участке 4-1 равна:

.

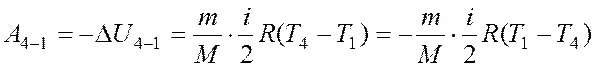Так как Т₁ = Т₂, а Т₃ = Т₄, то А_{2 - 3} = -А_{4 - 1}, т.е. полная работа по адиабатическому сжатию и расширению равна нулю.

Следовательно, работа цикла: А = А_1-2 – А_3-4.

Из уравнений (1), (2) и (5) получим: 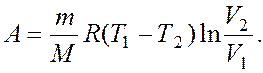       (7)

Из уравнения (6) выразим разность температур Т₂ – Т₃, равную Т₁ – Т₃, и подставим в уравнение (7): 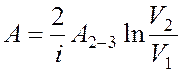. Произведем вычисления: .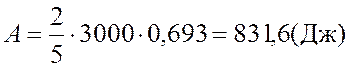

Ответ: 831,6 Дж.                   

Задача 17. В результате изотермического расширения объем 8 г кислорода увеличился в 2 раза. Определить изменение энтропии газа.

Дано: M = 32 кг/кмоль V2 = 2V1	Решение: Изменение энтропии системы определяется по формуле:         (1) где  dQ– количества тепла,
∆S - ?

сообщенное газу, Т – абсолютная температура, S₁ и S₂ – значения энтропии в начальном и конечном состояниях системы.