|
Дано: V= 50 м3 Ρ = 767 мм. рт. ст. @ 767·133 Па Т = 291 К М = 2 кг/моль |
Решение: На основании уравнения Менделеева – Клайперона:
|
|
ν – ? N – ? ρ – ? d – ? |
можно определить ν:
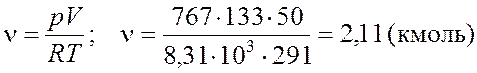
Число молекул N, содержащихся в данном объеме, находим, используя число Авогадро NА (которое определяет какое количество молекул содержится в одном киломоле). Общее количество молекул, находящихся в массе m данного газа, может быть установлено, так как известно число молей ν.
![]()
Подставляя в формулу число киломолей, устанавливаем
число молекул, содержащихся в объеме V: ![]() .
.
Плотность газа ρ = m/Vопределяем из уравнения Менделеева - Клайперона:
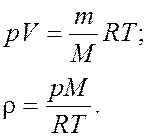
Подставляя числовые значения в единицах СИ в формулу, определим плотность газа:
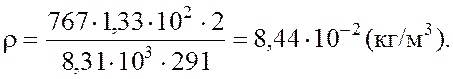
Удельный объем газа d определяем из уравнения Менделеева - Клайперона:
|
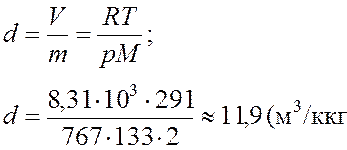
Ответ: 11,9 м3/кг.
Задача 2. В сосуде объемом 2 м3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
|
Дано: V= 2 м3 m1= 4 кг М1= 4·10-3 кг/кмоль m2= 2 кг М2= 2·10-3 кг/кмоль Т1= 300 К |
Решение: Воспользуемся уравнением Менделеева - Клайперона, применив его к гелию и водороду:
где р1 – парциальное давление гелия; m1 – масса гелия; |
|
р - ? М - ? |
М1 – егомолярная масса; V – объем сосуда; Т – температура газа; R= 8,31 Дж/(моль·К) –молярная газовая постоянная; р2 – парциальное давление водорода; m2 – масса водорода; М2 – его молярная масса.
По закону Дальтона: ![]() (3)
(3)
Из уравнений (1) и (2) выразим р1 и р2 и подставим в уравнение (3):
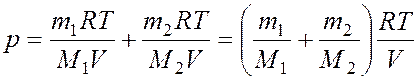 (4)
(4)
С другой стороны, уравнение Менделеева - Клайперона для смеси газов имеет вид:
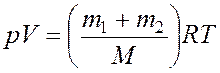 (5)
(5)
Сравнивая (4) и (5) найдем молярную массу смеси газов по формуле:
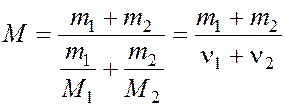 ,
(6)
,
(6)
где ν1 и ν2 – число молей гелия и водорода соответственно.
|
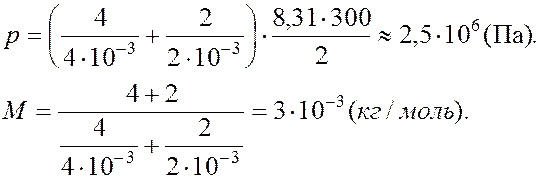
Ответ: 3·10-3 кг/моль.
Задача 3. При каком давлении средняя длина свободного пробега молекул водорода <λ> = 2,5 см при температуре 68°С? Диаметр молекул водорода принять равным d = 2,3·10 –10 м.
|
Дано: <λ>= 2,5·10-2 м Т= 341 К d= 2,3·10-10 м NA = 6,02·1026 кмоль-1 |
Решение: Давление водорода при температуре Т можно найти по уравнению Менделеева- Клайперона, в котором удобно ввести число молекул n0 в 1 м3. |
|
р – ? |
Это проводится следующим образом:
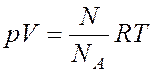 ;
; 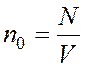 ;
; 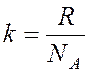 ;
;
где NA – число Авогадро и k – постоянная Больцмана.
Следовательно, 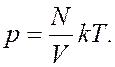 Так
как
Так
как 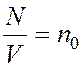 , имеем
, имеем ![]() .
.
Число молекул в 1 м3 выразим через среднюю длину свободного пробега. Из формулы 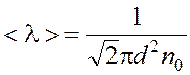 , находим
, находим 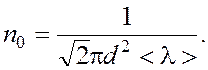 Таким образом:
Таким образом:
|
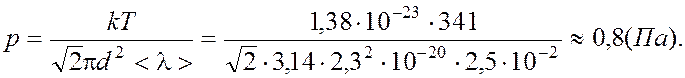
Ответ: 0,8 Па.
Задача 4. Определить плотность разреженного азота, если средняя длина свободного пробега молекул 10 см. Какова концентрация молекул?
|
Дано: < λ >= 10 см = 0,1 м |
Решение: Средняя длина пробега молекулы определяется формулой: |
|
р - ? n0 - ? |
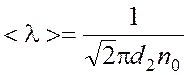 , (1)
, (1)
где d– эффективный диаметр молекул (для азота d = 0,31·10 –9 м).
Концентрацию молекул найдем из равенства:
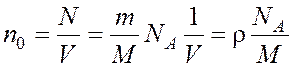 , (2) где
NA – число
Авогадро; М= 28·10 –3 кг/моль – молярная масса
азота.
, (2) где
NA – число
Авогадро; М= 28·10 –3 кг/моль – молярная масса
азота.
Решая совместно уравнения (1) и (2), находим: 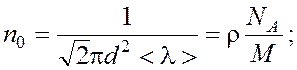
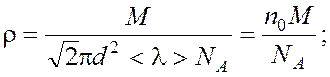
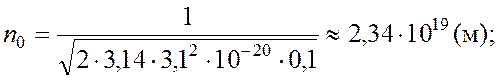
|
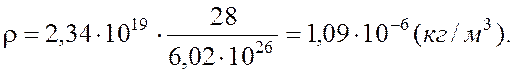
Ответ: 1,09·10-6 кг/м3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.