Основы молекулярной физики и термодинамики: Методические указания к практическим занятиям по курсу общей физики, страница 4

Дано: Р1 =100 кПа=1·105 Па Р2 = 1 МПа =1·106 Па V2 = const g = 1,4 Р3 – ?

Решение: На PV диаграмме представлен график, соответствующий процессу, указанному в условии задачи.

Процесс адиабатического сжатия 1-2 совершается без теплообмена и согласно уравнению Пуассона:  

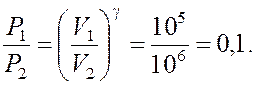                                                                    (1)

Макроскопические параметры P, V, T  воздуха в состоянии 1, 2, 3  связаны соотношением:

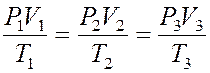, откуда      P₁V₁ = P₃V₃.

По условию задачи V₂ = V₃. Используя уравнение (1) можно записать

.

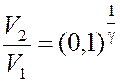Тогда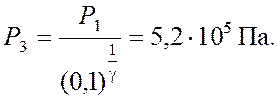                                      

Ответ:  

Задача 9. Вычислить массу столба воздуха высотой 1 км и сечением  1 м², если плотность воздуха у поверхности Земли  а давление Р₀ = 1,013 ∙ 10⁵ Па. Температуру воздуха считать одинаковой.

Дано: h = 1 км = 1000 м S = 1 м2 Т= const Р0=1,013 ∙ 105 Па  = 1,2 кг/м 3	Решение: Атмосферное давление меняется с высотой, плотность воздуха также является функцией высоты . Массу воздуха в элементе объема dV представим в виде: dm=  . Найдем изменение плотности воздуха с высотой.
m – ?	Согласно уравнению состояния идеального газа

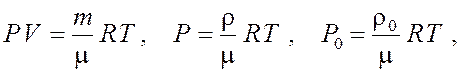
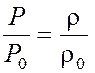                                               .                                            (1)

Продифференцировав (1), получим 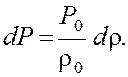                               (2)

С другой стороны убыль давления  dP  при переходе от высоты  h₀ к высоте h₀ + dh

                                        (3)

где – плотность воздуха на высоте h.

Используя уравнения (2)  и  (3) получим:

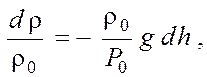
или

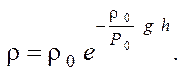
Вычислим массу столба воздуха

Подставив данные, приведенные в условии задачи получим:

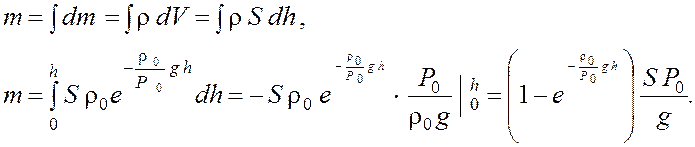
m = 1,13 · 10³ кг.

Ответ:     m = 1,13 · 10³ кг.

Задача 10. Определить скорость вылета поршня массой 4 кг из цилиндра при адиабатном расширении кислорода в 40 раз, если начальное давление воздуха 10⁷ Па, а объем 0,3 л.

Дано: Т = 4 кг V2/V1 = 40 p1 = 10 7Па V1 = 0,3 л = 3·10-4 м3	Решение: Работа А, совершаемая адиабатически расширяющимся воздухом, в данном случае идет на увеличение кинетической энергии поршня, т. е
υ - ?

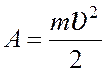, где т и υ – масса и скорость поршня.

Для подсчета работы адиабатически расширяющегося газа воспользуемся формулой: 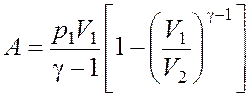, где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме (для кислорода γ =1,4).

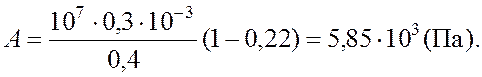 Так как 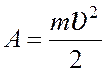, то ,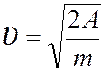   

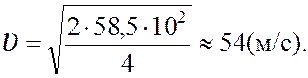
Ответ: 54 м/с.

Задача 11. Молекулярный пучок кислорода ударяется о неподвижную стенку. После соударения молекулы отражаются от стенки с той же по модулю скоростью. Определить давление пучка на стенку, если скорость молекул 500 м/с и концентрация молекул в пучке 5·10 ²⁴ м ^-3.

Дано: υ = 500 м/с n0 = 5·10 24 м –3	Решение: Давление определяется по формуле:         ,                             (1)
р - ?

где F – сила давления, S – площадь.

Силу давления найдем из второго закона Ньютона:  

 ,                                       (2)

где m – масса кислорода, ударившегося о стенку за время t,               Δυ – изменение скорости молекул при ударе.

Массу одной молекулы кислорода найдем из закона Авогадро: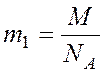, где М = 32·10²³ кг/моль – молярная масса кислорода; N_A = – постоянная Авогадро.

За время t о стенку ударяются молекулы, находящиеся в объеме: , масса которых: .                     (3)

Изменение скорости при соударении:.        (4)

Подставляя выражения (3), (4) в (2), находим: 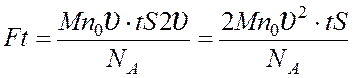, откуда , .

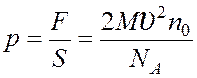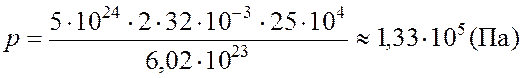Ответ: 1,33·10⁵ Па.

Задача 12. Определить удельные теплоемкости с_р, с_v, для смеси 1 кг азота и 1 кг гелия.

Дано: m1= 1 кг                  М1= 28 кг/кмоль i1 = 5 m2 = 1 кг М2= 4 кг/кмоль газа. i2  = 3	Решение: Удельной теплоемкостью какого – либо газа называется величина, равная количеству теплоты, которое нужно сообщить единице массы тела, чтобы повысить его температуру на 1 градус. При этом величина теплоемкости зависит от условий, при которых
ср - ? сv - ?