Основы молекулярной физики и термодинамики: Методические указания к практическим занятиям по курсу общей физики, страница 3

Задача 5. Вычислить коэффициент внутреннего трения и коэффициент диффузии кислорода, находящегося при давлении 0,2 МПа и температуре 280 К.

Дано: p = 2·105 Па d= 2,9·10-10 м М = 32·10-3 кг/моль Т = 280 К	Решение: На основании представлений молекулярно – кинетической теории газов коэффициент внутреннего трения идеального газа (динамическая вязкость) и коэффициент диффузии определяются по формулам:
η - ? D - ?

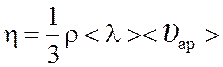 (1); 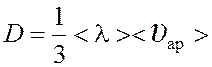         (2), где ρ – плотность газа; < λ > – средняя длина свободного пробега молекул; <υ_ар> – средняя арифметическая скорость молекул.

Из (1) и (2) следует                                                (3)

Среднюю арифметическую скорость и среднюю длину свободного пробега молекул находим по формулам:

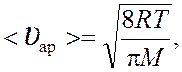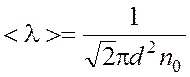     (4)         ,    (5)

где R = 8,31 Дж/(моль·К) – молярная газовая постоянная; Т – термодинамическая температура; d = 2,9·10 ^–10 м – эффективный диаметр молекулы кислорода; n₀ – число молекул в 1 м³ (концентрация).

Из уравнения Менделеева - Клайперона определяем n₀

 (см. задачу 3): 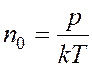                                                       (6)

где р – давление; k = 1,38·10 ^–23 Дж/К – постоянная Больцмана.

Подставляя (6) в уравнение (5), получаем: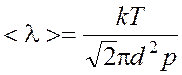 .                                     (7)

Окончательный вид расчетной формулы для коэффициента диффузии найдем, подставляя выражения (4) и (7) в уравнение (2):

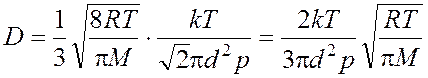.      (8)

Плотность кислорода определяется по формуле: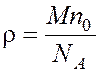. С учетом (6) имеем:  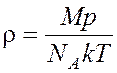          .                                       (9)

Подставляя (9) и (8) в (3), получаем расчетную формулу для коэффициента внутреннего трения:   .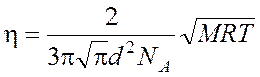

Вычисляем: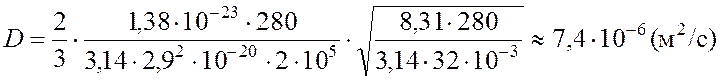       

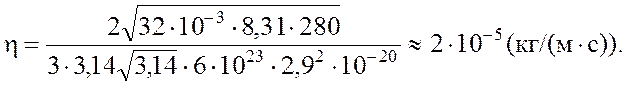
Ответ: .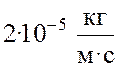

Задача 6. Наружная поверхность кирпичной стены площадью 25 м² и толщиной 37 см имеет температуру 259 К, а внутренняя поверхность–293 К. Помещение отапливается электроплитой. Определить ее мощность, если температура в помещении поддерживается постоянной. Теплопроводность кирпича      0,4 Вт/(м·К).

Дано: S = 25 м2 D = 37 см = 0,37 м T1 = 259 K T2 = 293R χ= 0,4 Вт/(м·К)	Решение: Количество теплоты, прошедшее через наружную стену, определим по закону Фурье:             (1) где t – время протекания теплоты.
N - ?

За время t – электроплита должна выделить такое же количество теплоты:                                                                                                (2)

Приравнивая правые части уравнений (1) и (2), получаем:

                                                 ,

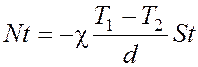откуда  ,    

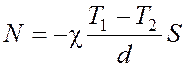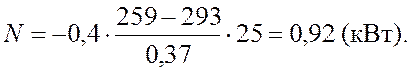
Ответ: 0,92 кВт.

2. Основы термодинамики

Задача 7. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К.

Дано: т = 2 кг Т = 400 К М = 2·10 –3 кг/моль	Решение: Считаем водород идеальным газом. Молекула водорода – двухатомная. Связь между атомами считаем жесткой, тогда
<Eпост> - ?  <Eвр> - ?

число степеней свободы молекулы водорода равно 5. В среднем на одну степень свободы приходится энергия: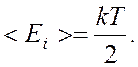 Поступательному движению приписывается три (i = 3), а вращательному две (i= 2) степени свободы. Тогда энергия одной молекулы:

,    .

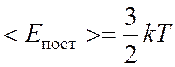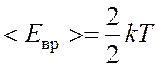Число молекул, содержащихся в массе газа m: 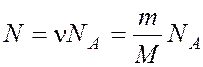 ,  где ν – число молей, N_A – число Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул водорода будет: 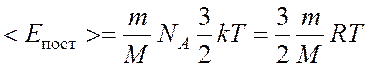  ,   (1) где R = kN_A – молярная газовая постоянная.

Средняя кинетическая энергия вращательного движения молекул водорода: 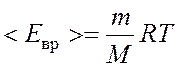            .                               (2)

Подставляя числовые значения и формулы (1) и (2), имеем:

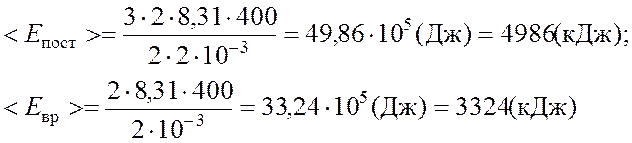
Ответ: 4986 кДж,   3324 кДж.

Задача 8. При адиабатическом сжатии давление воздуха было увеличено от Р₁ = 100 кПа  до  Р₂ = 1 МПа.  Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление Р₃ газа в конце процесса.