Решенная контрольная работа по факторному моделированию, страница 6

Оценка достоверности полученной модели

 

Оценим достоверность полученного уравнения, используя корреляционный анализ. Расчеты представлены в таблице 1.

 

Коэффициент парной корреляции определяет, взаимосвязаны ли два фактора.

 

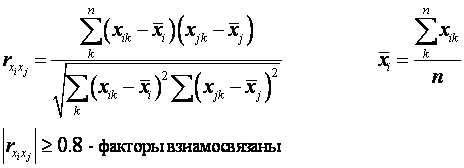    r_{z x1}=0,9139/√(2,1085*0,4677)=0,9203 >0,8 Следовательно, z и х₁ взаимосвязаны;

   r_{z x2}=5,7132/√(2,1085*24,0548)=0,8022 >0,8                       z и х₂ взаимосвязаны;

     r_x1x2=2,3493/√(0,4677*24,0548)=0,7004 <0,8             х₁ и х₂  не взаимосвязаны.

 

Таблица 2 Матрица коэффициентов парной корреляции

 

 

Коэффициент детерминации отображает полноту охвата характеризующих факторов:

 

D=1-0.054/0.51=0.8941. Следовательно, на 89,4% изменение результирующего фактора z зависит от факторов x₁ и x₂, а на 10,6% - от неучтенных факторов.

 

Множественный коэффициент корреляции R характеризует, насколько правильно мы выбрали конкретный вид зависимости:

 

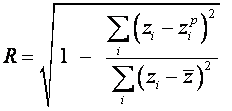
Если множественный коэффициент корреляции R стремится к 1,  значит, зависимость выбрана правильно.

 

R=√(1-0,054/0,51)=0.9456

 

Среднеквадратичное отклонение  определяет точность зависимости:

 

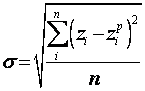s =√(0,22/21)=0.1023

 

Так как множественный коэффициент корреляции R стремится к 1 (0,9456), зависимость выбрана правильно. Таким образом, полученная модель позволяет определить значение результирующего показателя с точностью ±0,1023.

Поскольку результирующий показатель в рассматриваемом примере - экзаменационная оценка, то такая точность полученной зависимости приемлема.

О=0,307^1,4940,092.