Решенная контрольная работа по факторному моделированию, страница 4

Метод наименьших квадратов заключается в нахождении таких параметров выбранной зависимости, при которых сумма квадратов отклонений расчетных значений функции от фактических, называемая функцией ошибки, минимальна.

 

 

Метод наименьших квадратов применим к  формальным зависимостям, которые линейны относительно своих параметров. Рассмотрим его применение на следующем примере:

                          

 

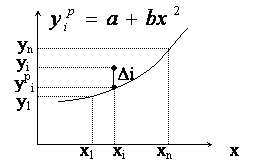
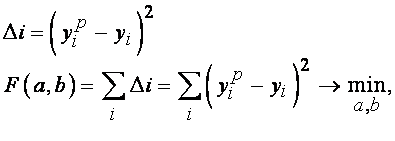
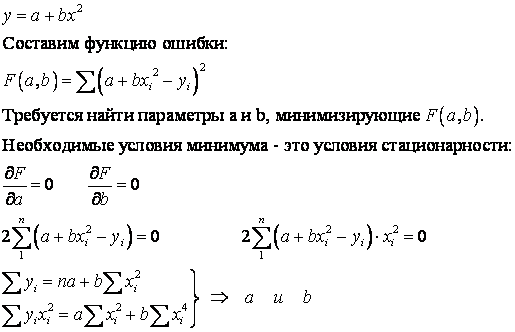Построение факторной модели

 

Имеются следующие исходные данные, где в квадратных скобках указано максимально возможное количество посещений лекций П_max, а количество строк в исходных данных соответствует количеству студентов в группе:

 

Необходимо определить вид зависимости. Для этого нужно  последовательно выполнить три этапа построения факторной модели.

В результате этого выбираем зависимость, имеющую следующий вид: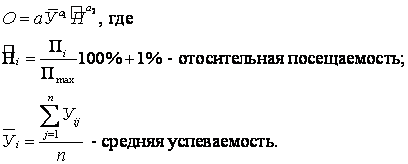

Необходимо составить уравнение регрессии, связывающее значение случайных величин с вполне определенными (детерминированными) значениями исходных параметров.

Наиболее распространенным приемом составления уравнений регрессии является метод наименьших квадратов.

Чтобы применить метод наименьших квадратов, нужно выбранную зависимость привести к линейному виду.

 

Поскольку выбранная формальная зависимость степенная, то, чтобы привести ее к линейному виду, ее нужно прологарифмировать, в результате чего получим:

Заполняем таблицу 1 расчетными значениями.

В нашем примере n=21 (количество студентов).

Получаем следующую систему уравнений:

Решив эту систему методом Гаусса, находим значения параметров А, а₁ и а₂:

                    А== -1,179;              ==1,494;              ==0,092.

Таким образом, z= -1,179 + 1,494х₁ + 0,092х₂

Вернемся к прежним переменным: lnО = -1,179 + 1,494ln + 0,092.

Чтобы прийти к выбранному виду зависимости, находим:

а=ехр(А)=ехр(-1,179)=0,307

Отсюда О=0,307^1,4940,092.