Используя граничные
условия (1.22) и (1.23), получаем с учетом соотношений (3.9) систему линейных
алгебраических уравнений относительно ![]() и
и ![]() :
:
![]()
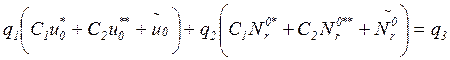 ,
,![]()
(3.10)
где ![]() .
.
Решая систему (3.10), находим постоянные интегрирования.
Для
сокращения объема вычислений при численном решении рассматриваемой краевой
задачи целесообразно так назначить начальные векторы ![]() ,
,
![]() ,
, ![]() , чтобы
одна из постоянных интегрирования
заведомо
обращалась в нуль.
, чтобы
одна из постоянных интегрирования
заведомо
обращалась в нуль.
Систему (3.10) можно представить в следующем виде:
![]()
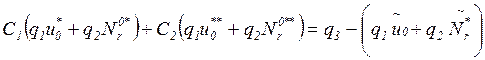 ,
,![]()
(3.11)
Для того,
чтобы ![]() при любых значениях достаточно выполнения
следующих соотношений:
при любых значениях достаточно выполнения
следующих соотношений:
![]()
![]() ,
,
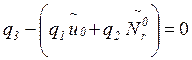
(3.12)
Выражение ![]() не может одновременно обратиться в нуль ввиду линейной независимости векторов
не может одновременно обратиться в нуль ввиду линейной независимости векторов ![]() ,
, ![]() .
.
Соотношения
(3.12) будут выполнены, если при ![]() принять
принять
![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е.
, т.е.
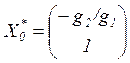 ,
, 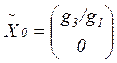 .
.
(3.13)
Если ![]() , то необходимо, чтобы
, то необходимо, чтобы ![]() . В противном случае из соотношения (1.22)
следует, что одновременно и
. В противном случае из соотношения (1.22)
следует, что одновременно и ![]() , а это означает, что
граничное условие на внутреннем контуре диска обращается в тождество и
решение задачи становится неопределенным.
, а это означает, что
граничное условие на внутреннем контуре диска обращается в тождество и
решение задачи становится неопределенным.
В случае, когда ![]() и
и ![]() , для
выполнения соотношений (3.12) можно принять
, для
выполнения соотношений (3.12) можно принять ![]() ,
, ![]() ;
; ![]() ,
, ![]() , т.е.
, т.е.
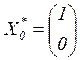 ,
, 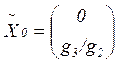 .
.
(3.14)
При указанном
выборе начальных векторов ![]() и
и ![]() равенство
равенство ![]() выполняется
при любых значениях исходных данных, и для решения рассматриваемой краевой
задачи достаточно выполнить численное решение только двух задач Коши:
выполняется
при любых значениях исходных данных, и для решения рассматриваемой краевой
задачи достаточно выполнить численное решение только двух задач Коши:
- для
системы однородных уравнений (3.4) при начальном векторе ![]() ;
;
- для
системы неоднородных уравнений (3.1) при начальном векторе ![]() .
.
Постоянную интегрирования ![]() в этом
случае определяем по формуле
в этом
случае определяем по формуле
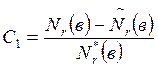
(3.15)
Вектор
решения краевой задачи находим затем по формуле (3.5), учитывая, что ![]() :
:
![]()
(3.16)
Изложенный метод можно применить также для расчета дисков без центрального отверстия.
По условиям
симметрии радиальное перемещение центра сплошного диска ![]() ,
т.е. коэффициенты
,
т.е. коэффициенты ![]() ,
, ![]() ,
, ![]() в условии (1.22) принимают значения:
в условии (1.22) принимают значения: ![]() ,
, ![]() .
.
При расчете сплошного диска формируем начальные векторы по формулам (3.13):
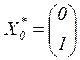 ,
,
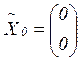
и выполняем численное
решение задач Коши для системы однородных уравнений (3.4) и системы
неоднородных уравнений (3.1) при начальных условиях ![]() и
и
![]() соответственно.
соответственно.
При численном
интегрировании матрицу коэффициентов ![]() и вектор
и вектор ![]() в точке
в точке ![]() формируем
в соответствии с уравнениями (1.39):
формируем
в соответствии с уравнениями (1.39):
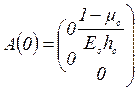
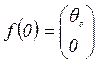
(3.17)
В точках ![]() элементы матрицы
элементы матрицы ![]() и
вектора
и
вектора ![]() вычисляем в соответствии с выражениями
(3.2) и (3.3).
вычисляем в соответствии с выражениями
(3.2) и (3.3).
Постоянную
интегрирования ![]() и решение краевой задачи
и решение краевой задачи ![]() для сплошного диска находим по формулам
(3.15) и (3.16), как и для диска с центральным отверстием.
для сплошного диска находим по формулам
(3.15) и (3.16), как и для диска с центральным отверстием.
Алгоритм численного решения краевой задачи для диска можно представить в более компактной форме. Введем в рассмотрение матрицы:
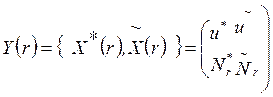 ,
,
(3.18)
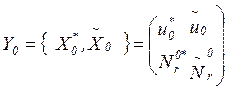
(3.19)
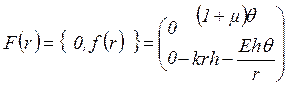 ,
, 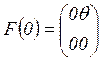 .
.
(3.20)
Столбцами
матрицы ![]() служат векторы
служат векторы ![]() и
и ![]() частных решений задач Коши для систем
(3.4) и (3.1). Матрица
частных решений задач Коши для систем
(3.4) и (3.1). Матрица ![]() состоит из векторов
начальных условий
состоит из векторов
начальных условий ![]() и
и ![]() .
Столбцами матрицы
.
Столбцами матрицы ![]() являются нулевой вектор и вектор
являются нулевой вектор и вектор ![]() ,
учитывающий массовые силы инерции и температурную деформацию диска в соответствии
с выражениями (3.3) и (3.17).
,
учитывающий массовые силы инерции и температурную деформацию диска в соответствии
с выражениями (3.3) и (3.17).
Решение краевой задачи для диска сводится к решению задачи Коши для дифференциального уравнения
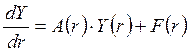
(3.21)
при начальном условии ![]() . В уравнении (3.21)
. В уравнении (3.21) ![]() - матрица, элементы которой определяются
выражениями (3.2) и (3.17). Численное интегрирование уравнения (3.21) выполняем
методом Рунге-Кутта:
- матрица, элементы которой определяются
выражениями (3.2) и (3.17). Численное интегрирование уравнения (3.21) выполняем
методом Рунге-Кутта:
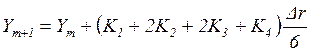 ;
;
![]() ,
,
(3.22)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() –
матрицы производных частных решений, определяемые выражениями:
–
матрицы производных частных решений, определяемые выражениями:
![]() ,
,
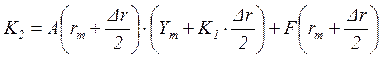 ,
,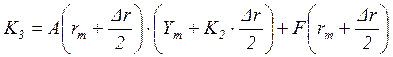 , ,
, , ![]()
(3.23)
В результате
находим матрицы частных решений ![]() ,
, ![]() , ... ,
, ... , ![]() уравнения
(3.21) в точках
уравнения
(3.21) в точках ![]() ,
, ![]() , … ,
, … ,![]()
![]() интервала
интервала ![]() .
.
Постоянную
интегрирования ![]() определяем по формуле
определяем по формуле
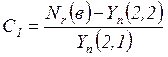 ,
,
(3,24)
где ![]() ,
, ![]() - элементы
второй строки матрицы
- элементы
второй строки матрицы ![]() (первая цифра в скобках
указывает номер строки, вторая - номер столбца матрицы),
(первая цифра в скобках
указывает номер строки, вторая - номер столбца матрицы), ![]() - радиальное усилие при
- радиальное усилие при ![]() .
.
Вектор решения краевой задачи для диска находим по формуле
![]() ,
,
![]()
![]() ,
,
(3.25)
где ![]() ,
, ![]() - соответственно первый и второй столбцы матрицы
- соответственно первый и второй столбцы матрицы ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.