Информатика и выч. техника \ Методы и алгоритмы расчетов на прочность в САПР

Расчет на прочность вращающихся дисков машин: Курс лекций, страница 3

В результате посадки диска на вал с натягом  (напомним,  что под натягом понимают разность диаметров вала и отверстия) на поверхностях контакта возникают силы давления.  Предположим,  что эти силы равномерно распределены по контактным поверхностям; интенсивность их обозначим через  и назовем контактным давлением. Величина контактного давления зависит от величины  натяга  угловой скорости вращения диска .

В основу расчета диска положим два допущения.  Согласно  первому принимаем равномерное распределение  напряжений по  толщине диска.  Согласно второму допущению предполагаем, что напряжения в плоскостях,  параллельных срединной плоскости, отсутствуют.  Это позволяет считать напряженное состояние всех точек диска двухосным.

Эти допущения были обоснованы путем сопоставления приближенного решения с точным, полученным для некоторых частных случаев, и справедливы при условии, что отношение внешнего диаметра диска к его наибольшей толщине больше 4.

Учитывая первое допущение,  заключаем,  что в рассматриваемой постановке  напряжения,  деформации и перемещения в диске являются функциями только радиуса.

Переходим к решению задачи.

1.2. Уравнение  равновесия элемента диска


Выделим из диска элемент в форме криволинейного шестигранника (рис. 1.2).  В радиальных сечениях по условиям симметрии касательные напряжения отсутствуют,  и возникают лишь нормальные напряжения,  которые  называются кольцевыми или окружными и обозначаются . Таким образом, площадки, лежащие в радиальных сечениях, являются

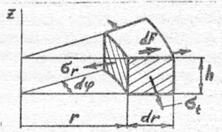
Рис.1.2. Элемент

диска


главными. Учитывая, что напряженное  состояние диска является плоским (см. второе допущение),  заключаем,  что площадки, лежащие  в окружных сечениях,  также являются главными.  Нормальные напряжения в этих сечениях называются радикальными и обозначаются .

Помимо радиальных и кольцевых внутренних сил к рассматриваемому элементу приложена еще и объемная сила  где объем элемента.


Внутренние силы,  возникающие в сечениях диска приводим к его срединной плоскости.  В окружном сечении получаем радиальное усилие интенсивности

на единицу длины окружного сечения срединной плоскости (рис.1.3). В радиальном сечении получаем кольцевое усилие интенсивности

на единицу длины радиального сечения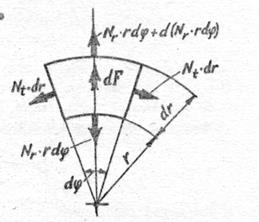

Рис.1.3. Внутренние

усилия в диске


срединной плоскости.

Проектируя силы, действующие на элемент диска,  на радиальное направление,  получим следующее уравнение равновесия:

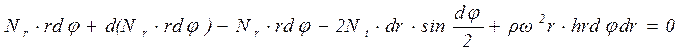
откуда,  учитывая,  что 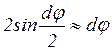  и обозначая , устанавливаем,  что


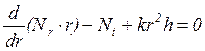
 (1.1)


Остальные уравнения равновесия для элемента выполняются тождественно.  Параметр  называют динамическим коэффициентом.

В уравнение равновесия (1.1) входят две неизвестных величины  и , поэтому задача определения внутренних усилий в диске является статически неопределимой. Для решения ее необходимо рассмотреть деформации.

1.3. Деформации элемента диска



Рассмотрим элемент диска до и после деформации  (рис.1.4). Перемещения точек диска по условиям


симметрии будут происходить в радиальных направлениях,  радиальное  перемещение  точек  на радиусе  обозначим через . Тогда радиальное  перемещение точек на радиусе  будет .  За положительное  направление для  примем направление от оси диска. Обозначим через  и  относительные деформации в диске в радиальном и кольцевом  направлениях и выразим их через  перемещение .

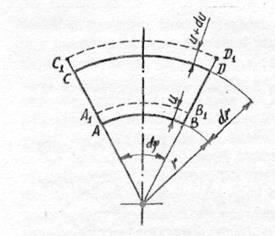
Рис.1.4. Перемещения точек элемента диска


Очевидно,  что радиальная деформация


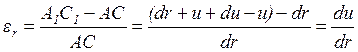
(1.2)


а кольцевая деформация


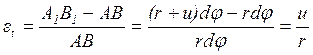
(1.3)


1.4. Связь между деформациями и внутренними усилиями в диске

Три  независимых уравнения (1.1) - (1.3) содержат пять неизвестных величин: , , , , . Недостающие два уравнения  получаем,  рассматривая обобщенный  закон Гука для материала диска. Поскольку напряженное  состояние является двухосным,  деформации и напряжения связаны следующими зависимостями:


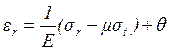
(1.4)



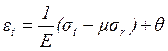
(1.5)


где   - температурная деформация, обусловленная нагревом диска на ; - начальная температура равномерно нагретого диска (обычно принимают ).  Температурная деформация определяется  по формуле:

Скачать файл