Расчет на прочность вращающихся дисков машин: Курс лекций, страница 4

(1.6)

Переходя в уравнениях (1.4) и (1.5) от напряжений  и  к усилиям  и ,  получаем

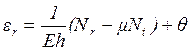
(1.7)

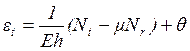
(1.8)

1.5.  Разрешающая система уравнений

для диска с  центральным отверстием

Уравнения (1.1) - (1.3), (1.7), (1.8) позволяют получить полное решение задачи о расчете напряженно-деформированного состояния диска. Примем в качестве  основных неизвестных радиальное перемещение  и радиальное усилие  и преобразуем эти уравнения, исключив из них величины , , .

Из уравнений (1.7) и (1.8) следует, что

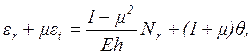
(1.9)

(1.10)

Подставляя соотношение (1.10) в уравнение (1.1), получаем

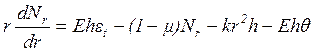
(1.11)

Заменяя в уравнениях (1.9) и (1.11) и  их выражениями (1.2) и (1.3), получаем систему линейных дифференциальных уравнений первого  порядка относительно  и :

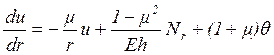
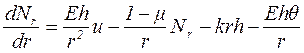(1.12)

В общем случае систему (1.12) интегрируем численным методом с применением ЭВМ. Постоянные интегрирования определяем из граничных условий на внутреннем и наружном контурах диска.

Через величины  и , определяемые из системы (1.12), можно выразить остальные параметры, характеризующие напряженно-деформированное состояние диска: 

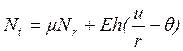
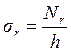
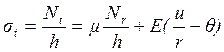
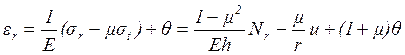
(1.13)

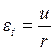
1.6.  Граничные условия

В случае, когда величина контактного усилия  на внутреннем контуре диска задана, граничное условие можно записать в следующей форме:

(1.14)

где ,  - радиальное усилие и толщина диска на внутреннем контуре.

При установке диска на вал с натягом величина контактного давления зависит от величины натяга , угловой скорости вращения , неравномерного нагрева диска и заранее неизвестна. Запишем уравнение совместности перемещений контактных поверхностей диска и вала:

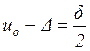
(1.15)

где  и  радиальные  перемещения точек поверхностей контакта диска и вала соответственно. Эти перемещения считаются положительными, если они направлены от центра.

Радиальные перемещения точек поверхности вала определяются выражением

(1.16)

где  - перемещения точек поверхности вала за счет контактного давления;

 - температурная деформация вала;  - коэффициент линейного расширения материала вала;  - температура нагрева вала;  - начальная температура вала (обычно ).

Перемещения точек посадочной поверхности вала за счет контактного давления  можно найти по формуле

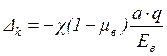
(1.17)

где ,  - модуль упругости и коэффициент Пуассона материала вала; - коэффициент, зависящий от отношения длины посадочной поверхности к диаметру вала; численное значение можно определить по формулам 

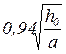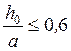       при ;

    при .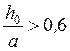

(1.18)

Подставляя выражения (1.16) и (1.17) в уравнение (1.15) и принимая во внимание, что контактное давление  связано с радиальным усилием  на внутреннем контуре диска соотношением (1.14), получаем

;

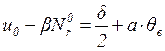(1.19)

где

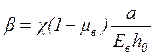
(1.20)

Соотношение (1.19) служит граничным условием в случае посадки диска на вал с натягом.

Если контактное давление между валом и внутренней поверхностью диска отсутствует (например, образуется зазор), граничное условие на внутреннем контуре диска принимает вид:

(1.21) 

В общем случае граничное условие на внутреннем контуре диска можно записать в форме

,

(1.22)

где , ,  заданные коэффициенты.

Граничное условие (1.14) можно получать из общего выражения (1.22) при , , . В случае посадки диска на вал с натягом , , 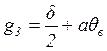. Граничное условие (1.21) получим из выражения (1.22) при , . Граничное условие на наружном контуре диска :

,

(1.23)

где  и  - радиальное усилие и толщина диска при ,  - интенсивность инерционной радиальной нагрузки, распределенной по наружной поверхности диска.

Совокупность уравнений (1.12), (1.13) и граничных условий (1.22), (1.23) является математической моделью напряженно-деформированного состояния вращающегося неравномерно нагретого диска с центральным отверстием.

1.7.  Сплошной диск

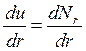Уравнения (1.12) остаются справедливыми и для сплошного диска (без центрального отверстия) кроме точки . Найдем производные  в центре диска,  полагая,  что они непрерывны в этой точке.

Разложим функцию в ряд по степеням  в окрестности точки :