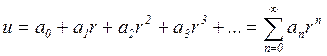Расчет на прочность вращающихся дисков машин: Курс лекций, страница 5

.

(1.24)

По условиям симметрии , следовательно, .

Подставляя разложение (1.24) в выражения (1.2) и (1.3), получаем

,

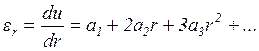(1.25)

,

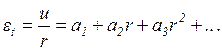(1.26)

Из выражений (1.25), (1.26) следует, что величины , ,  принимают в центре диска  одно и то же значение:

.

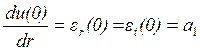(1.27)

Выразим усилия  и через деформации  и , воспользовавшись соотношениями (1.7) и (1.8):

,

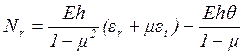(1.28)

.

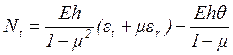(1.29)

Подставляя в выражения (1.28) и (1.29) разложения (1.25) и (1.26), находим

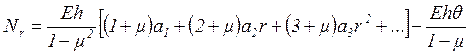
(1.30)

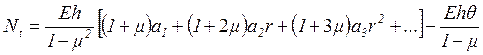
(1.31)

Из выражений (1.30) и (1.31) вытекает, что усилия  и  принимают в центре диска одно и то же значение :

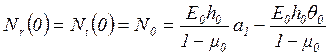
(1.32)

где , , ,  - значения соответствующие параметров при .

Из выражений (1.27) в (1.32) находим

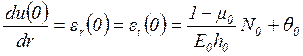
(1.33)

Найдем производную  из выражения  (1.30):

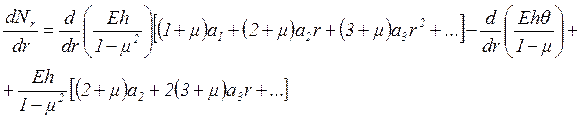
(1.34)

Полагая, что в центре диска производные 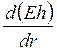 , ,  обращаются в нуль,  находим значение производной  в этой точке:

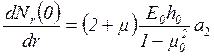
(1.35)

Уравнение (1.1) можно записать в следующем виде:

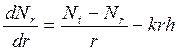
(1.36)

Подставляя в уравнение (1.36) выражения (1.30) и (1.31), получаем

,

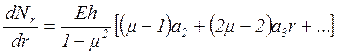(1.37)

откуда

.

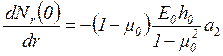(1.38)

Сопоставляя выражения (1.35) и (1.38), заключаем, что .

Таким образом, в центре диска

,

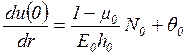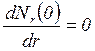
(1.39)

Расчет сплошного диска сводится к интегрированию системы (1.12), при этом производные   и  в точке  определяем по формулам (1.39). Для определения постоянных интегрирования служат граничные условия:

,

(1.40)

Отметим, что граничное условие в точке  можно получить из общего выражения (1.22) при , . Параметры, характеризующие напряженно-деформированное состояние в сечениях диска при , находим по формулам (1.13). Напряжения и деформации в центре диска определяем по формулам:

,

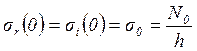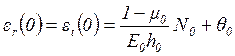
(1.41)

Уравнения (1.12), (1.13), (1.39), (1.41) и граничные условия (1.40) составляют математическую модель напряженно-деформированного состояния вращающегося сплошного неравномерно нагретого диска.

2.  РАСЧЕТ ДИСКОВ ПОСТОЯННОЙ ТОЛЩИНЫ

Для дисков постоянной толщины при , можно получить замкнутое решение задачи.

2.1.  Диск с центральным отверстием

При решении системы уравнений (1.1) - (1.3), (1.7), (1.8) применяем метод начальных параметров. Согласно этому методу постоянные интегрирования выражаем через начальные параметры  и  - радиальное перемещение и радиальное усилие, соответствующие внутреннему контуру диска.

Из уравнений (1.7) и (1.8) вытекает, что

.

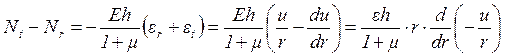(2.1)

Подставляя выражение (2.1) в уравнение (1.1), получаем

.

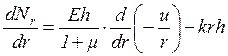(2.2)

Интегрируя уравнение (2.2) в промежутке от  до текущего значения , находим

,

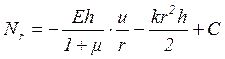(2.3)

.

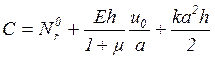(2.4)

Подставляем выражение (2.3) в первое уравнение системы (1.12):

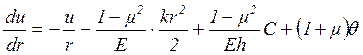
(2.5)

Принимая во внимание, что 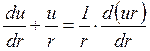, получаем

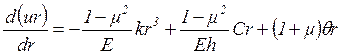
(2.6)

Интегрируем уравнение (2.6) в промежутке от  до :

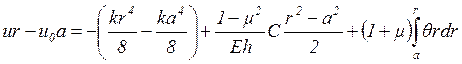
(2.7)

Подставляя в уравнение (2.7) выражение (2.4) для , получаем

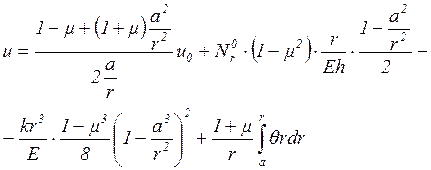
(2.8)

Подставляя выражение (2.8) в уравнение (2.3), находим

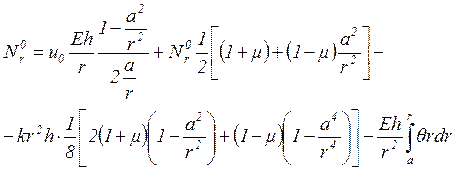
(2.9)

Введем обозначения: 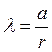  и

,       ,

,           ,

,          .

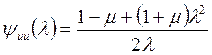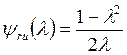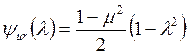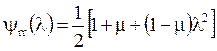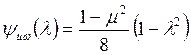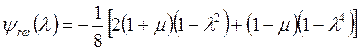Тогда уравнения (2.8) и (2.9) можно записать в следующем виде:

,

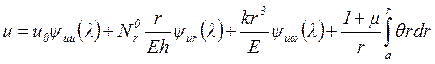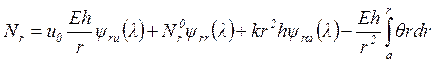
(2.10)

Уравнения системы (2.10) являются основными при расчете дисков постоянной толщины с нейтральным отверстием. Начальные параметры ,  определяем из граничных условий (1.22), (1.23).

Функции , , , ,,   называются сопровождающими функциями для диска. Их числовые значения для  приведены в приложении.

2.2. Сплошной диск

Основные уравнения для диска без центрального отверстия получаем из уравнений (2.8) и (2.9), выполняя в этих уравнениях предельный переход при и принимая во внимание, что для сплошного диска , .

Предварительно находим, используя соотношение (1.33),

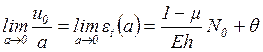
(2.11)

Переходя к пределу при  в уравнениях (2.8) и (2.9), получаем с учетом выражения (2.11):

,

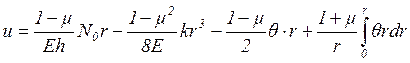(2.12)

.

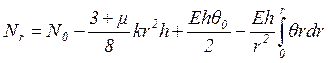(2.13)