Прогнозирование и планирование использования городских территорий, страница 14

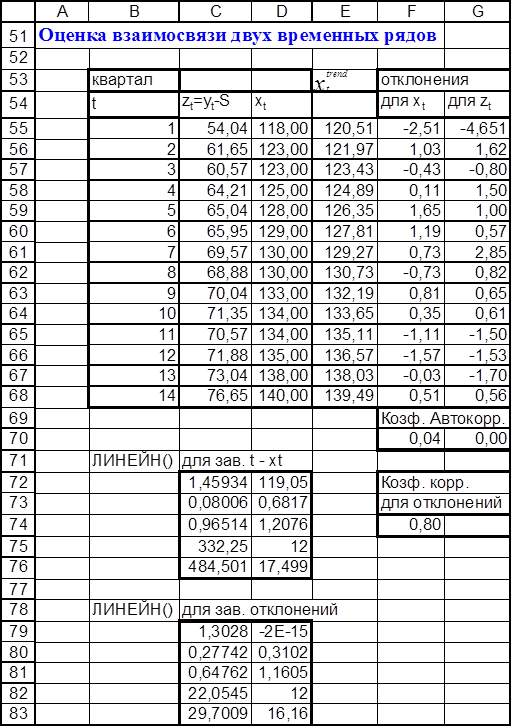
Поэтому, при исследовании взаимосвязи y_t и x_t , заменим ряд Y рядом (T+E) равным z_t=y_t-S_i , эти значения вычислены раннее и содержатся в интервале (H27:H40). Поскольку ряд X  не содержит циклической составляющей, то его преобразовывать не следует. Для того чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь, следует избавиться от ложной корреляции, вызванной наличием тенденции в каждом ряде. Это можно проделать, например, методом отклонений от трендов/

. Для ряда  x_t   с помощью функции ЛИНЕЙН(результат в интервале С72:D76 Рис.П1.5) построим уравнение регрессии

Используя его, можно получить расчетные значения  x_t^trend для каждого момента времени (интервал ячеек E55:E68).

.Приложение 2

Пример оформления задания 1 контрольной работы 2 в Excel

Таблица 1.

Исходные данные

№	Площадь территории района, га (bi)	1 этап		2 этап
		Элитное, dj=5,0	Средний класс, dj=2,5	Элитное, dj=5,0	Средний класс, dj=2,5
		Удельные затраты на строительство, $./м2
1	200	125	122	85	90
2	130	100	111	62	70
3	300	125	125	80	90
4	80	120	115	75	80

Математическая модель задачи описывается уравнениями (2.1)-(2.4). Эти уравнения определяют задачу линейного программирования.

Соотношение (2.1) определяет целевую функцию. Формулы (2.2) и (2.3) определяют фазовые ограничения, а соотношение (2.4) –естественные ограничения. Задачу линейного программирования может быть решена различными способами. Рассмотрим ее решение в  Excel c помощью надстройки Поиск Решения:

1.  Разместим на рабочем листе MS Excel исходные данные, как показано на рис.П.2.1. Искомые значения переменных разместим в ячейках B11:С14 ; F11:G14.В начальный момент их можно положить равными 0. Значение целевой функции (затраты инвестора) для данной задачи вычисляется как сумма инвестиций по двум этапам. Для вычисления суммы инвестиций разместим величины удельных затрат на первом (I) и втором (II) этапах в интервалах B5:C8 и F5:G8 соответственно.  Сумма инвестиций по I этапу содержится в ячейке B19 и может быть вычислена по формуле =СУММПРОИЗВ(B5:C8;B11:C14).  Сумма инвестиций по II этапу вычисляется аналогично, поэтому в ячейке записана формула =СУММПРОИЗВ(F5:G8;F11:G14).  Значение целевой функции содержится в ячейке J19 вычисляется по формуле =B19+F19.

Ограничение  (2.2) в данном случае определяет два неравенства, каждое из которых обеспечивает величину застройки по всем участкам  не меньше чем план на каждом из этапов. Для вычисления   левой части неравенства в ячейку B17 заносится формула =СУММ(B11:C14), в ячейку F17 заносится формула =СУММ(F11:G14).  Плановые показатели 400 и 600 на каждом из этапов заносятся в D17 и H17 соответственно.

Ограничение (2.3) в данном случае определяет четыре неравенства , каждое из которых обеспечивает не превышение суммарной площади территории по всем видам жилья по обеим этапам  территории возможного размещения новой застройки для каждого из участков. Внесем нормативы использования территории 5 и 2.5 в ячейки B9 и C9 соответственно. Территория, занятая жилой застройкой на Участке 1 на I  этапе, может быть вычислена по формуле СУММПРОИЗВ($B$9:$C$9;B11:C11), которая заносится в ячейку D11. Ячейки D12:D14 содержат аналогичные формулы, которые позволяют вычислить территорию, занятую жилой застройкой на I  этапе на каждом из Участков 2,3 и 4 .