При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня зависят от предыдущих. Для измерения автокорреляции уровней ряда заполним интервал B3:H18 рабочего листа (рис.П1.1).. Первые два столбца содержат исходные данные, а последующие - уровни ряда, сдвинутые на один шаг во времени. Определим коэффициент автокорреляции первого порядка (коэффициент корреляции между рядами yt и yt-1.) с помощью встроенной функции Excel КОРРЕЛ(), результат запишем в ячейку D20. Коэффициенты автокорреляции последующих порядков вычисляются аналогично и заносятся в ячейки E20:H20. Поскольку наиболее высокое значение имеет коэффициент автокорреляции 4-го порядка, можно сделать вывод о наличии циклических колебаний с периодичностью в 4 квартала. Заметим, что наличие таких колебаний обусловлено предметной сущностью рассматриваемого ряда - сезонным изменением спроса
 |
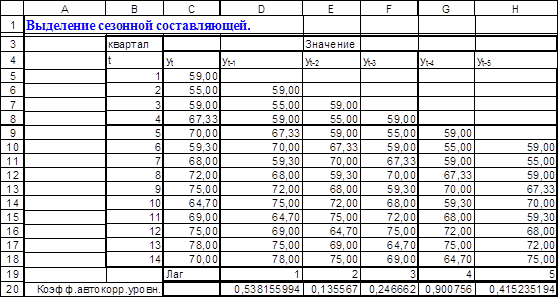Рис.П1.1.
Также отметим, что коэффициент автокорреляции первого порядка достаточно велик, что позволяет сделать вывод о том, что рассматриваемый ряд содержит тенденцию.
Анализ структуры временных рядов, содержащих сезонные и циклические колебания может быть проведен с помощью аддитвной модели временного ряда. Общий вид аддитивной модели
 |
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Получение выровненных данных (T+E) .
4. Аналитическое выравнивание уровней (T+E)
5. Расчет значений T.
6. Расчет полученных по модели значений (T+S)
7. Расчет абсолютных и относительных ошибок.
Выполнение этих шагов показано в интервале B25:L40 (рис.П1.2).
Шаг 1.
а) Найдем скользящие средние по формуле D28:D38 за каждые 4 квартала;
б)Найдем центрированные скользящие центрированные средние (по формуле )E29:D38 .
Шаг 2.
Найдем оценки сезонной компоненты, как разность между фактическими уровнями ряда и скользящими центрированными средними по формуле F29:F38.
Используем эти оценки для расчета сезонной компоненты S. (Фрагмент таблицы A42:F49 Рис.П1.3.).
Шаг 3.
Вычленим влияние сезонной компоненты (H27:H40) (рис.П1.2). T+E=yt-Si
Шаг 4. Используя функцию ЛИНЕЙН (интервалI44:J48 (рис.П1.3). проведем аналитическое выравнивание ряда (T+E)
Таким образом, имеем следующий линейный тренд.
 |
Используя это уравнение, найдем значения T для каждого момента времени I27:I40 (рис.П1.3).
Шаг 6.
Используя это уравнение, найдем значения (T+S) для каждого момента времени J27:J40 (рис.П1.3).
Шаг 7.
Используя это уравнение, найдем значения E=Y-(T+S) для каждого момента времени K27:K40 (E-абсолютная ошибка для каждого квартала). Сумма квадратов абсолютных ошибок находится в ячейке L41.
Сумма квадратов отклонений yt от его среднего может быть вычислено с помощью формулы =КВАДРОТКЛ(C27:C40). Эта величина равна 632.90 Относительная ошибка равна 56,86/632,90*100=8,83%.
Т.е. можно сказать, что 91% общей вариации уровней временного ряда объясняется предложенной моделью.
 |
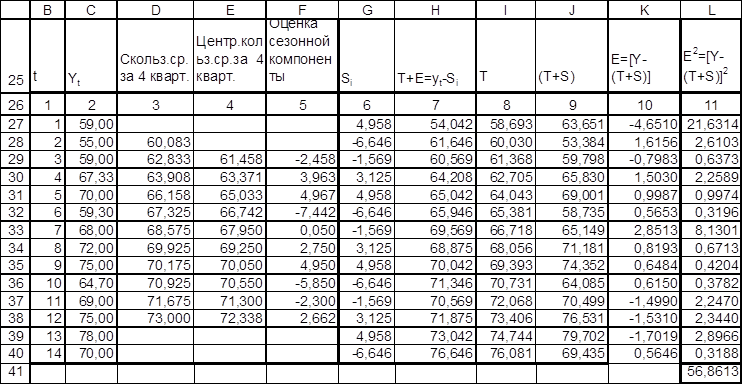Рис.П1.2.
 |
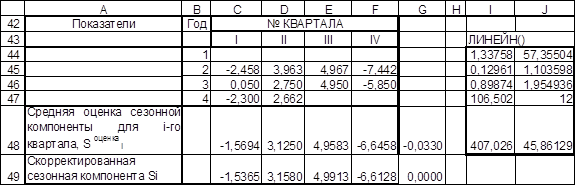Рис.П1.3
На Рис.П1.4 приведены графики исходных зависимостей yt и xt, а также тенденция Tи сумма тенденции и сезонной составляющей (T+S) зависимости yt
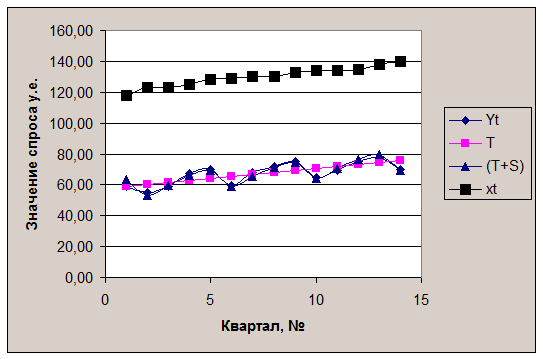Рис.П1.4
Визуальный анализ зависимости xt от t, проведенный по этому же рисунку, показывает отсутствие циклической составляющей в этой зависимости.
Оценка взаимосвязи двух временных рядов
Специфика статистической оценки взаимосвязи двух рядов (в отличии от традиционных методов корреляционно-регрессионного анализа) заключается в том, что перед проведением исследования необходимо устранить сезонную (циклическую) составляющую. Наличие последней может привести к искажению истинных показателей силы и тесноты связи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.