Особенности реализации трехшаговых итерационных методов.Факторизация, страница 7

5.2 Исследования на несимметричных матрицах

5.2.1 Исследования на 7- ми диагональных матрицах

Для исследования были выбраны СЛАУ со следующими матрицами и векторами правых частей:

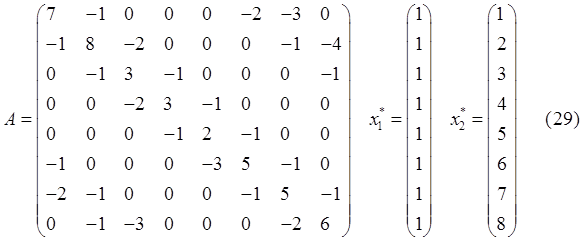
Результаты вычислений для СЛАУ (29) приведены в таблице (5.1). Быстрее всех здесь сходится метод LU(sq)MSG. Здесь больше всего обращает на себя внимание тот факт, что методы LOS и DiagLOS не сходятся на СЛАУ с такой матрицей. Невязка с некоторого момента становится постоянной и не достигает заданной. Не помогает даже увеличение максимально возможного числа итераций. В этой ситуации мы поступили следующим образом. В качестве начального приближения для нового итерационного процесса мы брали старое решение, на котором останавливался итерационный процесс. В результате после применения такой процедуры 4-5 раз методы LOS и DiagLOS все-таки сошлись на СЛАУ с точным решением . На СЛАУ же с точным  решением подобного рода процедура не помогает сходимости метода LOS. Невязка в этом случае начинает постепенно уменьшаться, но делает это очень медленно. В принципе, для избавления от такого рода эффектов нужно делать число допустимых итераций побольше, и через определенное число итераций нужно обновлять начальное приближение и невязку, начиная итерационный процесс заново, но с новым начальным приближением, являющимся текущим решением предыдущей итерации.

Были проведены и исследования на следующих СЛАУ:

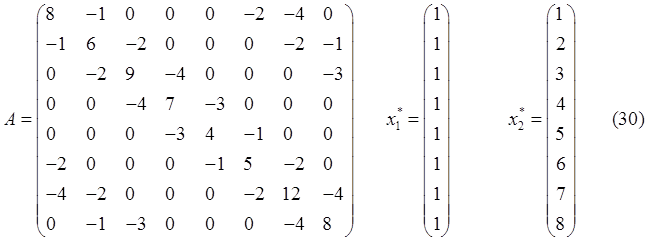
Результаты вычислений для данной СЛАУ приведены в таблице 5.2. Как видим из этой таблицы, эффекта с постоянной невязкой, который присутствовал при решении предыдущих СЛАУ здесь не наблюдается. Быстрее всех сходятся методы c неполной факторизацией и MSG_trans. На этом тесте с помощью неполной факторизации удается добиться заметного преимущества. Кроме того при исследовании метода MSG_trans наблюдалось скачкообразное поведение невязки, причем ее порядок менялся от  до . Для метода сопряженных градиентов это нормальная ситуация , поэтому выход из итерационного процесса для этого метода по числу итераций бессмыслен, т.к. эти колебания невязки вообще говоря не являются затухающими.

Кроме того, были проведены исследования на СЛАУ с матрицами вида (29) и (30) с обратным  знаком вне диагональных элементов. Результаты вычислений приведены в таблицах (5.3) и (5.4). Поскольку они ничем принципиальным не отличаются от результатов таблицы 5.2, мы оставляем их без комментариев.

5.2.2 Исследования на плотных матрицах

Для исследования была выбрана СЛАУ со следующей матрицей:

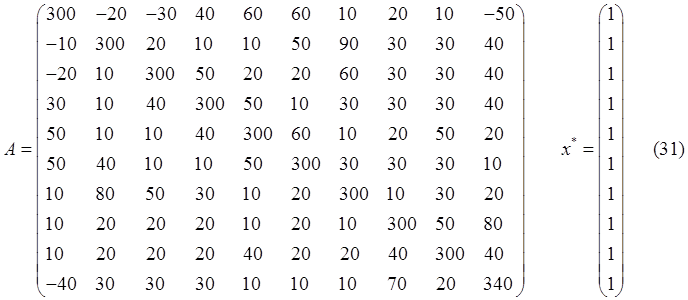
Результаты вычислений приведены в таблице 6. Они ничем принципиально не отличаются от результатов пункта 5.1.3, поэтому мы оставляем их без комментариев. Стоит лишь отметить, что медленнее всех сходится метод MSG_trans, да и решение он дает с большей погрешностью, чем остальные методы. Связано это с тем, что использование этого метода увеличивает число обусловливания матрицы СЛАУ. Подобный результат наблюдается и в предыдущем пункте. 

Замечание к пункту  5

1.  Во многих таблицах приведена не только обыкновенная невязка, но и предобусловленная. В некоторых случаях она больше обыкновенной, а в некоторых меньше на 1-2 порядка. Это еще раз доказывает необходимость выхода из итерационного процесса по обыкновенной невязке, т.к. предобусловленная невязка может сделать выход из итерационного процесса задолго до того, как получено решение с нужной точностью.