В этом
случае поступаем аналогично пункту 2.3.3. Для реализации используется схема
(21), только в качестве матриц ![]() и
и ![]() выбираются диагональные матрицы, на
диагоналях которых стоят квадратные корни из соответствующих диагональных
элементов матрицы
выбираются диагональные матрицы, на
диагоналях которых стоят квадратные корни из соответствующих диагональных
элементов матрицы ![]() .
.
Замечания:
1. В дальнейшем этот метод мы будем сокращенно обозначать DiagLOS.
2.7 Оценка количества действий у исследуемых методов.
Подсчитаем количество действий, которое требуется на выполнение одной итерации у исследуемых методов. Причем за действие будем считать только скалярное произведение.
Это
связано с тем, что за одну итерацию в основном выполняются только скалярные
произведения. Поэтому это действие и примем за единицу счета. Умножение матрицы
на вектор эквивалентно ![]() скалярным произведением. В тех
методах, где используется неполная факторизация, действия, затраченные на саму
факторизацию, не учитываются.
скалярным произведением. В тех
методах, где используется неполная факторизация, действия, затраченные на саму
факторизацию, не учитываются.
Из
лабораторной работы 1 известно, что на прямой и обратный ход тратится ![]() арифметических действий. Учитывая, что на
скалярное произведение тратится
арифметических действий. Учитывая, что на
скалярное произведение тратится ![]() арифметических действий,
будем считать, что на прямой и обратный ход тратится
арифметических действий,
будем считать, что на прямой и обратный ход тратится ![]() скалярных
произведений. Кроме того, мы не будем учитывать скалярные произведения, которые
тратятся на инициализацию векторов
скалярных
произведений. Кроме того, мы не будем учитывать скалярные произведения, которые
тратятся на инициализацию векторов ![]() ,
, ![]() и др. С учетом этих предположений имеем
и др. С учетом этих предположений имеем
MSG:
![]()
DiagMSG:
![]()
MSG_trans:
![]()
LU(sq)MSG:
![]() (22)
(22)
LU_diagMSG:
![]()
LOS:
![]()
LU(sq)LOS:
![]()
DiagLOS: ![]()
Эти значения непосредственно получаются из формул, соответствующих данным методам.
Замечания:
1.
При подсчете
количества действий у методов с диагональным предобусловливанием мы полагали,
что на решение СЛАУ с диагональной матрицей тратится ![]() скалярного
произведения и округляли общее количество по правилам округления.
скалярного
произведения и округляли общее количество по правилам округления.
2.
Поскольку мы
будем сравнивать исследуемые методы и с методом блочной релаксации, то
необходимо знать количество действий на итерацию у этого метода. Из
лабораторной работы 2 известно, что в методе блочной релаксации на одну
итерацию тратится ![]() арифметических действий. С
учетом наших предположений будем считать, что на одну итерацию в методе блочной
релаксации тратится
арифметических действий. С
учетом наших предположений будем считать, что на одну итерацию в методе блочной
релаксации тратится ![]() скалярных произведений.
скалярных произведений.
3. Мы будем сравнивать исследуемые методы не только по количеству итераций, но и по общему времени, затраченному на получение приемлемого решения. На матрицах небольшой размерности это время не удается отследить функцией gettim, поэтому при анализе этих результатов мы будем учитывать количество действий на одну итерацию. При исследованиях на матрицах большой размерности это время отследить удается и мы будем сравнивать методы по времени.
3. Алгоритм реализации рассматриваемых методов
Все
используемые при реализации методов матрицы в памяти ЭВМ хранятся в
разреженно-строчном формате. Поэтому при использовании неполной ![]() факторизации это следует учитывать. Сама
факторизации это следует учитывать. Сама ![]() производится по следующим формулам:
производится по следующим формулам:
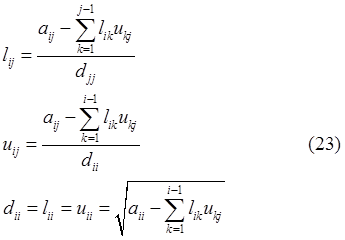
Алгоритм
неполной ![]() - факторизации практически ничем не
отличается от алгоритма полной факторизации, реализованного в лабораторной
работе 1. Единственное отличие заключается в том, что при накоплении суммы
скалярного произведения в формулах (23) перед каждым умножением проверяется
принадлежность пар индексов
- факторизации практически ничем не
отличается от алгоритма полной факторизации, реализованного в лабораторной
работе 1. Единственное отличие заключается в том, что при накоплении суммы
скалярного произведения в формулах (23) перед каждым умножением проверяется
принадлежность пар индексов ![]() и
и ![]() портрету матрицы
портрету матрицы ![]() (в
этом случае умножение возможно, в противном же случае соответствующее слагаемое
не вычисляется, т.к. оно является нулевым ). Кроме того, в случае
принадлежность пары
(в
этом случае умножение возможно, в противном же случае соответствующее слагаемое
не вычисляется, т.к. оно является нулевым ). Кроме того, в случае
принадлежность пары ![]() портрету матрицы
портрету матрицы ![]() соответствующие элементы матриц
соответствующие элементы матриц ![]() и
и ![]() вычисляются
по формулам (23), в противном же случае они принудительно полагаются равными
нулю.
вычисляются
по формулам (23), в противном же случае они принудительно полагаются равными
нулю.
С учетом формата хранения матрицы реализуются также прямой и обратный ход, а также умножение матрицы на вектор. В остальных подпрограммах никаких трудностей при реализации методов с учетом формата хранения не возникает.
4. Тестирование.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.