Особенности реализации трехшаговых итерационных методов.Факторизация, страница 6

Стоит также отметить, что и при переходе на двойную точность исследуемые методы значительно выигрывают по скорости сходимости у метода блочной релаксации, причем это преимущество стало еще значительнее.

5.1.3 Исследование на плотных матрицах

Для исследования была выбрана СЛАУ со следующей матрицей и вектором правой части:

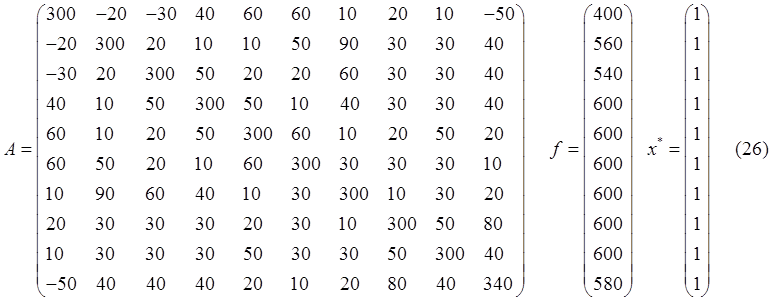
Результаты вычислений приведены в таблице (3). Как и ожидалось, методы LU(sq)LOS и LU(sq)MSG сошлись за одну итерацию. Наибольшее количество итераций дает метод LU_diagMSG. Стоит также отметить, что методы LOS и MSG сходятся за одинаковое количество итераций. Меньше всех действий на получение решения тратит метод LU(sq)LOS. Кроме того, из таблицы (3) видно, что здесь методы без предобусловливания уступают по скорости сходимости методам с предобусловливанием.

5.1.4 Исследование на матрицах большой размерности.

Исследования велись на 3-х диагональных и плотных матрицах большой размерности. 3-х диагональная матрица имеет следующий вид:

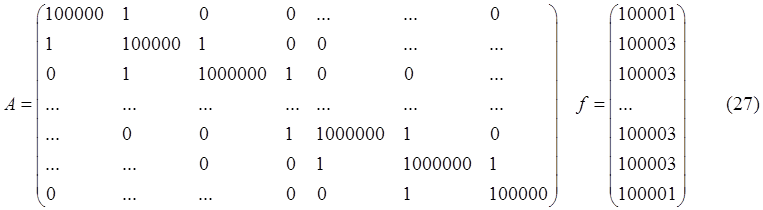
Результаты вычислений приведены в таблиц (4). Как видно из этой таблицы, все модификации LOS в среднем быстрее получают решение, чем MSG и его модификации (лишь в некоторых случаях MSG тратит меньше времени). Среди всех исследуемых методов быстрее всех (по времени) сходятся методы LOS и LU(sq)LOS. В целом же на рассмотренных матрицах не проявляется значительного преимущества какого-либо метода. Разница колеблется в пределах 0.05-0.5 секунды. При размерности  на решение СЛАУ методом LOS уходит около 1.5 часа, поэтому другие методы мы тестировать на этой размерности не стали. Такая длительность связана не только с самим методом, но и с тем, что при данной размерности матрица уже полностью не помещается в оперативную память ЭВМ (тестирование проводилось на ЭВМ с оперативной памятью в 256 Мб).

Плотная матрица большой размерности, на которой проводилось исследование, имеет следующий вид:

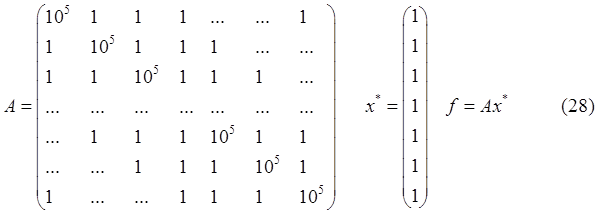
Результаты вычислений также приведены в таблице (4).  При  и  быстрее всех по времени сходится метод LOS. Метод MSG и методы с диагональным предобусловливанием уступают ему 0.01-0.02 с. Методы же с неполной факторизацией значительно уступают вышеупомянутым. Уже при   они сходятся за довольно большое время. В принципе, это нормальный результат. Методы LU(sq)LOS и LU(sq)MSG решение получают фактически прямым методом, т.к. в силу плотности матрицы неполная факторизация становится полной. Как известно, количество действий для прямого метода с -факторизацией есть . Поэтому при увеличении размерности матрицы в 10 раз, общее время получения решения увеличивается в 1000 раз. Именно по этой причине мы не стали использовать эти методы для решения СЛАУ с большими размерностями, потому что здесь их время работы будет измеряться часами. В принципе, при решении СЛАУ с плотными матрицами больших размерностей методы с неполной факторизации всегда будут работать достаточно долго, т.к. основная часть этого времени идет на неполную факторизацию матрицы.  При  и  классические методы и методы с диагональным предобусловливанием сходятся за почти одинаковое время. Однако уже при  мы видим преимущество классических методов. Стоит отметить, что все исследуемые методы сошлись за 1-2 итерации. В принципе, такой результат был предсказуем, т.к. на матрицах с таким явным диагональным преобладанием любой итерационный метод сойдется за 1-2 итерации (итерационные методы так и строятся, чтобы на таких матрицах сходиться за 1-2 итерации). Поэтому сравнение исследуемых методов по числу итераций на данном тесте бессмысленно. Мы же проводили данное тестирование с целью сравнения этих методов по времени.