Особенности реализации трехшаговых итерационных методов.Факторизация, страница 3

Тогда 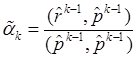. Кроме того . Домножим теперь обе части равенства (14.5) на . В результате с учетом (17.2) получим:

, или с учетом (17.1) и (17.3) . Введем в рассмотрение два дополнительных вектора:

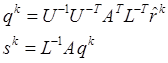
Тогда для выражения (14.6) будем иметь:

Отсюда получаем, что

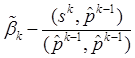
Преобразуем теперь выражение (14.7):

 

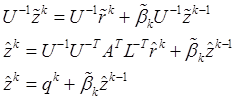
Кроме того

С учетом предпоследнего равенства имеем:

Таким образом, итерационный процесс (14.1) – (14.7) окончательно можно записать в виде:

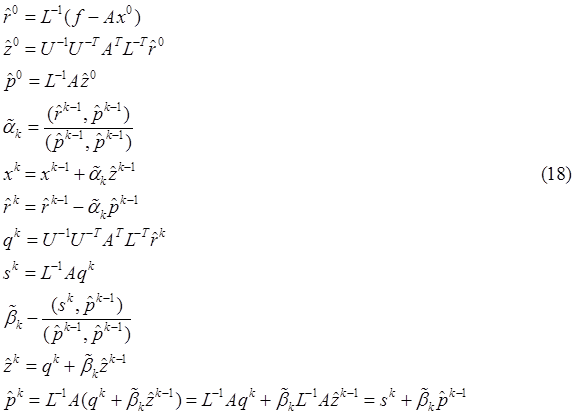
Именно эту схему мы и будем исследовать в дальнейшем. В качестве матриц  и  мы будем брать матрицы неполной - факторизации матрицы .

Замечания:

1. В дальнейшем эту схему мы будем сокращенно обозначать LU(sq)MSG.
2. При рассмотрении СЛАУ (12) мы подразумевали существование разложения . В дальнейшем, где будут использоваться матрицы  и , мы будем подразумевать их существование.
3. Неполная факторизация матрицы аналогична неполному разложению Холесского, только элементы матриц  и  строятся по формулам полной факторизации.
4. См. замечание (4) к пункту 2.2. Подобного рода замечание справедливо и к пунктам 2.3.3, 2.4 и  2.5.
5. Заметим, что здесь в качестве матрицы  можно взять матрицу . Действительно, матрица  все равно будет симметричной и положительно определенной.
6. Следует заметить, что в схеме (18) вычисляется предобусловленная невязка. Поэтому при реализации следует это учесть, и выход из итерационного процесса осуществлять по невязке исходной системы. В частности, из (18) видно, что .

2.3.3 Метод сопряженных градиентов с диагональным предобусловливанием при помощи неполной  - факторизации

Кроме классического метода диагонального предобусловливания существует и другой.  Он заключается в том, что для его реализации используется схема (18), только в качестве матриц  и  выбираются диагональные матрицы, на диагоналях которых стоят квадратные корни из соответствующих диагональных элементов матрицы . Преимущество этого метода перед классическим методом диагонального предобусловливания заключается в том, что он применим и для несимметричных матриц.

При реализации этого метода также стоит учесть, что в нем используется предобусловленная невязка.

Замечание:

1. В дальнейшем эту схему мы будем сокращенно обозначать LU_diagMSG.

2.4 Локально–оптимальная схема.

Кроме адаптации метода сопряженных градиентов существуют и специальные методы, применимые и к СЛАУ с несимметричными матрицами. Одной из таких схем является локально-оптимальная схема. Она имеет следующий вид:

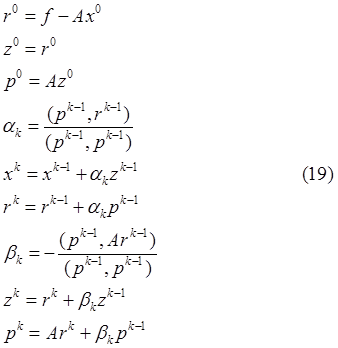
Итерационный процесс заканчивается, если величина  стала достаточно малой. При этом квадрат нормы невязки можно вычислять с помощью рекуррентного соотношения:

Замечание:

1.  В дальнейшем этот метод мы сокращенно будем обозначать LOS.

2.  Поскольку в дальнейшем мы будем сравнивать исследуемые методы между собой, то выходить из итерационного процесса мы должны по одинаковому условию для всех исследуемых методов. В качестве такого условия выберем условие достаточной малости относительной  невязки исходной системы (1) (не предобусловленной!) .

2.5 Локально-оптимальная схема с неполной - факторизацией

Будем теперь применять схему (19) к предобусловленной СЛАУ вида:

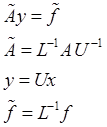
где  и  - матрицы неполной - факторизации. Тогда схема (19) переписывается в виде:

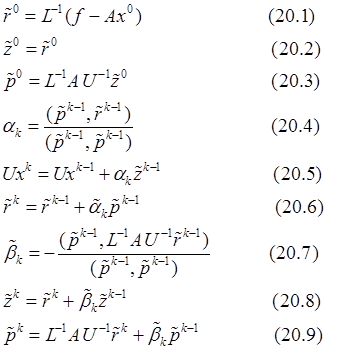
Преобразуем теперь эту схему к более удобному для практического применения виду. Для этого введем в рассмотрение вектора:

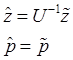
Тогда имеет место:

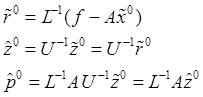
С учетом этих соотношений имеем:

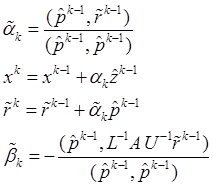
Домножив соотношение (20.8) на матрицу , получим:

Кроме того

Таким образом, схему (20.1) – (20.9) можно окончательно переписать в виде

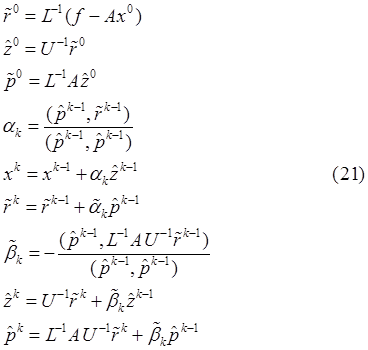
Замечания:

1.  В  дальнейшем этот метод мы сокращенно будем обозначать LU(sq)_LOS.

2.6 Локально-оптимальная схема с использованием диагонального предобусловливания.