Особенности реализации трехшаговых итерационных методов.Факторизация

1. Цель работы

Изучить особенности реализации трехшаговых итерационных методов для СЛАУ с разреженными матрицами. Исследовать влияние предобусловливания на сходимость изучаемых методов на нескольких матрицах большой (не менее 10000) размерности.

Задание: Сравнить МСГ и ЛОС для несимметричной матрицы. Факторизация .

2. Исследуемые методы

2.1 Метод сопряженных градиентов

Пусть дана СЛАУ

 

с симметричной, положительно определенной матрицей . Алгоритм классического метода сопряженных градиентов имеет следующий вид:

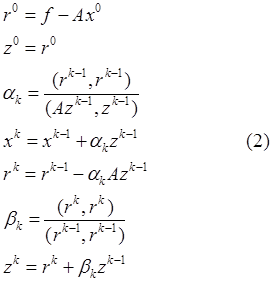
Здесь

- вектор начального приближения

-  вектор решения на - ой итерации

- вектор невязки на  - ой итерации

- вектор спуска (сопряженное направление) на - ой итерации                           

- коэффициенты.

Выход из итерационного процесса осуществляется либо при достаточной малости относительной невязки:

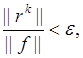
либо при превышении максимально допустимого числа итераций («аварийный» выход).

Существует и другая схема для реализации метода сопряженных градиентов. Она имеет следующий вид:

 

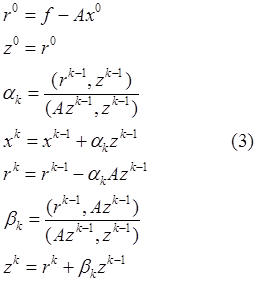
Замечание:

    1. В дальнейшем этот метод мы будем сокращенно обозначать MSG.

2.2 Метод сопряженных градиентов с диагональным предобусловливанием.

Пусть дана СЛАУ (1) с плохо обусловленной матрицей. Тогда решая ее методом сопряженных градиентов, мы затратим достаточно большое количество итераций для получения приемлемого по точности решения, а, следовательно, и времени. Попытаемся получить эквивалентную (1) СЛАУ, но уже с хорошо обусловленной матрицей. Тогда приемлемое по точности решение мы будем получать гораздо быстрее.

Пусть - некоторая невырожденная матрица. Домножив (1) на , получим систему

Система (3) имеет такое же точное решение , что и система (1). Перепишем (3) в виде

где

 

Хотя алгебраически системы (5) и (1) эквивалентны, спектральная характеристика матрицы в общем случае отличается от спектральной характеристики матрицы , что, вообще говоря, ведет к изменению скорости сходимости численного метода для (5) по отношению к (1). Процесс перехода от (1) к (5) с целью улучшения характеристик матрицы системы для увеличения скорости сходимости называется предобусловливанием. Одним из методов предобусловливания является так называемый метод неполной факторизации матрицы. Он заключается в том, что подбирается такая матрица , что , и при этом процедура решения СЛАУ вида  является не слишком трудоемкой. Пусть существует разложение . Если положить , то мы получим эквивалентную (1) СЛАУ:

Как видим, такой выбор матрицы не имеет смысла, т.к. задача сводится к решению СЛАУ прямым методом. Пусть теперь , где  - матрица неполного разложения Холесского (см. замечание). Перейдем от (1) к эквивалентной ей СЛАУ:

 

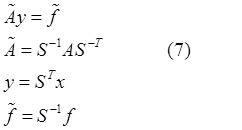
Прежде чем применять к этой СЛАУ схему (1), проверим, что матрица  симметричная и положительно определенная, иначе метод сопряженных градиентов неприменим. Действительно

Последний переход возможен в силу симметричности матрицы . Далее

Последнее неравенство справедливо в силу положительной определенности матрицы . Здесь мы воспользовались свойством сопряженного оператора с вещественнозначной матрицей (а именно  и ). Этим свойством мы будем пользоваться и в дальнейшем.

Перепишем теперь схему (2) для системы (7):

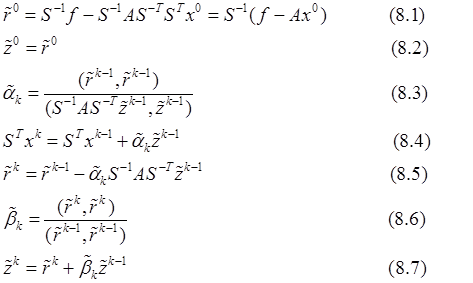
Попытаемся теперь преобразовать эту схему к более удобному для практического применения виду. Введем в рассмотрение следующие вектора:

 

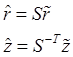
Тогда формулы (8.1) и (8.2) преобразуются к виду:

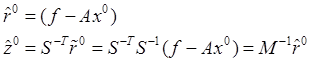
Далее:

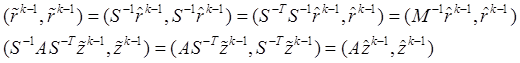
С учетом этих соотношений можно записать

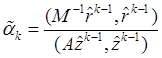
Домножив соотношение (8.4) на матрицу , а соотношение (8.5) на матрицу , получим:

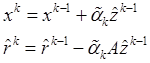
Далее:

С учетом этого соотношения (8.6) принимает вид:

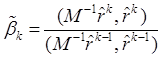
Домножим теперь (8.7) на матрицу . Имеем

Таким образом, схему (8.1) – (8.7) окончательно можно переписать в виде:

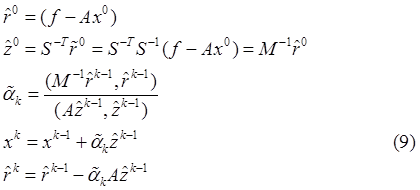
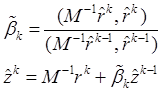
Мы в качестве выберем матрицу , где  - главная диагональ матрицы . Тогда схема (9) будет реализовывать диагональное предобусловливание системы (1).

Замечания:

1. В дальнейшем этот метод мы будем сокращенно обозначать DiagMSG.
2. Здесь и далее под эквивалентностью двух СЛАУ мы будем понимать алгебраическую эквивалентность. Ясно, что в спектральном плане они не эквивалентны. Именно поэтому используется предобусловливание.
3. Полагая , мы подразумевали. Что данное разложение существует.
4. Неполное разложение Холесского строится по формулам полного разложения Холесского с условием, что портрет матрицы  совпадает с портретом нижнего треугольника матрицы  , т.е. все ненулевые элементы, которые по формулам полного разложения Холесского получаются на месте нулевых (по портрету) элементов матрицы  принудительно задаются равными нулю. Неполное разложение Холесского можно записать в виде , где  - некоторая матрица с элементами, которые принудительно задавались равными нулю при неполном разложении. Поэтому в (7) мы полагаем и считаем (7) эквивалентной (1).
5. Заметим, что в качестве матрицы  в системе (7) нельзя взять матрицу , если к (7) мы собрались применять схему (2). Это следует из того, что матрица   не является симметричной, тогда как схема (2) применима только для симметричных, положительно определенных матриц. 
6. Нахождения произведения  для получения  в общем случае ведет к изменению портрета матрицы. Поэтому на практике это произведение явно не вычисляют, а учитывают при построении итерационного процесса (см. формулы