Особенности реализации трехшаговых итерационных методов.Факторизация, страница 5

Все программы были протестированы на двух основных категориях тестов: на тестах корректности данных и вычислительных тестах. При вводе некорректных данных программа корректно завершает свою работу (выдает сообщение о нехватке памяти, о несовпадении размерностей матрицы и вектора и т.д.) На вычислительных тестах программа также работает корректно (см. пункт 5). При не существовании разложения матрицы, делении на ноль выдается соответствующее сообщение.

5. Исследование методов

5.1 Исследования на симметричных матрицах

5.1.1 Исследование на 7-ми диагональных матрицах

 Для исследования были выбраны СЛАУ со следующими матрицами и векторами правых частей:

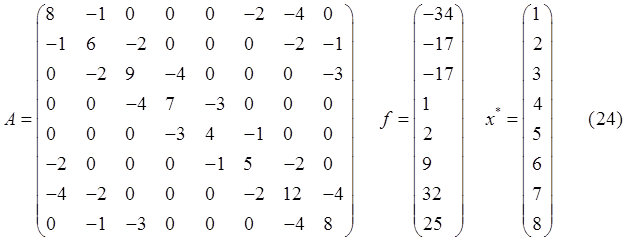
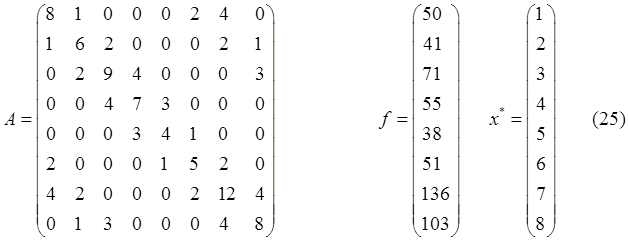
Здесь и далее  - точное решение. Результаты вычислений приведены в таблицах (1.1) и (1.2) (см. приложение 1). Как видно из этой таблицы, все рассмотренные методы по количеству итераций намного выигрывают у метода блочной релаксации (это с учетом того, что блочная релаксация за итерацию тратит меньше всего действий из рассматриваемых методов). Наименьшее количество итераций среди исследуемых методов тратит LU(sq)LOS, наибольшее же – LU_diagMSG. Однако если учитывать количество действий, затраченных на итерацию (плюс предобусловливание), то быстрее сходятся методы DiagLOS и DiagMSG. Уже на этом тесте видно, что предобусловливание не всегда приводит к увеличению скорости сходимости. На СЛАУ (25) это преимущество уже не так заметно. Блочная релаксация и исследуемые методы сходятся за примерно равно число итераций. Но если еще и учесть действия за итерацию, то блочная релаксация выигрывает по скорости у исследуемых методов. Среди исследуемых методов за наименьшее количество итераций по-прежнему сходится LU(sq)LOS. Однако с учетом действий за итерацию быстрее сходятся методы DiagLOS и DiagMSG. В принципе, без предобусловливания рассматриваемые методы могут проигрывать блочной релаксации (на этих приведенных тестах это не так заметно), однако предобусловливание позволяет  опережать блочную релаксацию по скорости сходимости.

Замечания:

1.  Все вычисления, там, где об этом специально не сказано, велись на REAL*4.

 5.1.2 Исследование на матрице Гильберта

Матрица Гильберта строится следующим образом:

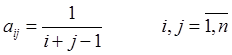
Исследования проводились при . Результаты приведены в таблицах (2.1) и (2.2).  На матрице размерности 4 все исследуемые методы тратят на порядок меньше действий, чем блочная релаксация. Быстрее всех сходятся методы LU(sq)LOS и LU(sq)MSG. Стоит также отметить, что несмотря на относительную невязку порядка , мы получаем в среднем 3-4 правильных знака в компонентах решения. Связано это с тем, что  матрицы Гильберта  плохо обусловлены. Их числа обусловленности:

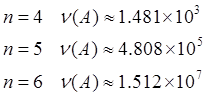
Поэтому, даже несмотря на маленькую невязку, мы получаем такую погрешность решения. Похожая ситуация наблюдается и при   и . Методы без неполной факторизации дают по–прежнему в среднем 3-4 правильных знака в компонентах решения, несмотря на увеличение числа обусловленности.  LU(sq)LOS и LU(sq)MSG при  дают решения с компонентами, вообще не имеющими правильных знаков. Если на всех методах мы ставили невязку , то на этих  мы специально ставили невязку . Делали мы это со следующей целью. При невязке  эти методы всегда сходились за оду итерацию, причем решение было с погрешностью, большей чем у остальных методов. Связано это с тем, что решение получалось не итерационным методом, а прямым (-разложением). Действительно, т.к. матрица Гильберта – плотная, то неполная факторизация переходит в полную. Поэтому уже на первой итерации мы получаем решение с невязкой порядка .  Ставя невязку на несколько порядков меньше, мы добиваемся выполнения нескольких итераций, получая уже решение не прямым методом, а итерационным. Однако, как видно из таблицы (1.2), при , даже  выполнив нескольких итераций, мы все равно получаем решение с компонентами, не содержащими ни одного правильного знака. Переходя же на двойную точность, при  уже получаем решение с 10 правильными знаками. Таким образом, при вычислениях на REAL*4 матрица Гильберта размерности 6 получается как бы вычислительно вырожденной, т.е. при решении СЛАУ с такой матрицей методами LU(sq)LOS и LU(sq)MSG для    погрешности не хватает знаков (она не помещается в разрядную сетку), поэтому она так быстро накапливается и мы получаем решение с довольно большой погрешностью. При переходе же на REAL*8 погрешность не накапливается гораздо  медленнее за счет увеличения разрядной сетки. Таким образом, решать СЛАУ с матрицей Гильберта размерности 6 и больше методами LU(sq)LOS и LU(sq)MSG необходимо на REAL*8.