Особенности реализации трехшаговых итерационных методов.Факторизация, страница 2

(9)).

7. В формулах (9) не требуется построение матрицы , а предполагается решение соответствующей СЛАУ с матрицей .
8. При преобразовании схемы (8.1) – (8.7) нам удалось привести ее к вполне компактному и удобному для практического применения виду. В общем случае не всегда удается это сделать, поэтому иногда схему вида (8.1) – (8.7) оставляют без изменений.

2.3 Метод сопряженных градиентов для решения СЛАУ с несимметричной матрицей.

2.3.1 Симметризация СЛАУ с помощью домножения на транспонированную матрицу

Если необходимо решать СЛАУ с несимметричной матрицей, то одним из вариантов может быть следующий. Так метод сопряженных градиентов применим только для симметричных, положительно определенных  матриц, то несимметричную систему необходимо преобразовать к симметричной с помощью некоторых эквивалентных преобразований. Это можно сделать, умножив слева систему на матрицу . В результате перейдем к новой СЛАУ:

, где

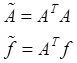
Матрица системы (10) будет симметричной, положительно определенной. Покажем это. Действительно, , что говорит о симметричности матрицы .

Положительная определенность матрицы  следует из того, что .

Построим теперь итерационную процедуру для системы (6). Естественно, что она должна строится так, чтобы не было необходимости хранить матрицу . Запишем схему (1) для системы (10):

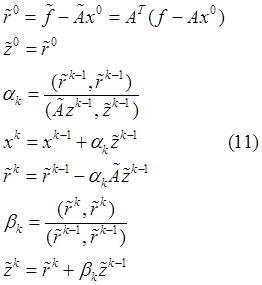
Замечания:

1. В дальнейшем этот метод мы будем сокращенно обозначать MSG_trans.
2. Рассмотренный выше метод симметризации СЛАУ часто является далеко не самым лучшим. Связано это с тем, что число обусловленности матрицы  равно квадрату числа обусловленности матрицы . Поэтому если исходная СЛАУ (1) была хорошо обусловленной, то СЛАУ (6) может быть плохо обусловленной, что влечет к появлению значительной погрешности в численном решении и достаточно медленной сходимости.
3. Выход из итерационного процесса (7) нужно делать не по малости невязки (невязка системы (10), предобусловленная невязка), а по малости невязки (невязка системы (1), истинная невязка). Связано это с тем, что невязка  может быть намного меньше невязки , что приведет к выходу из итерационного процесса задолго до того, как будет получено решение (1) с нужной невязкой. Поэтому при реализации схемы (7) мы будем это учитывать. Из (11) непосредственно следует, что . Этим соотношением мы и будем пользоваться для получения невязки системы (1).

2.3.2 Метод сопряженных градиентов для несимметричной СЛАУ  с использованием неполной - факторизации.

Рассмотрим другой способ перехода к СЛАУ с симметричной, положительно определенной матрицей. Будем решать вместо исходной СЛАУ (1) предобусловленную СЛАУ , в которой

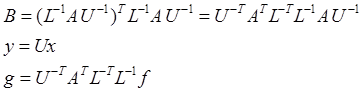
Здесь  и  - матрицы неполной факторизации исходной матрицы (см. замечание к этому пункту). Покажем, что  - симметричная, положительно определенная матрица. Действительно, вводя обозначение , получим , а значит  - симметричная, положительно определенная матрица (см. пункт 2.3.1). Таким образом, мы по сути применили описанный в п. 2.3.1 метод для предобусловленной  СЛАУ (1)  (с учетом  систему (1) можно записать ). Тогда для СЛАУ

схему (3) можно записать в виде:

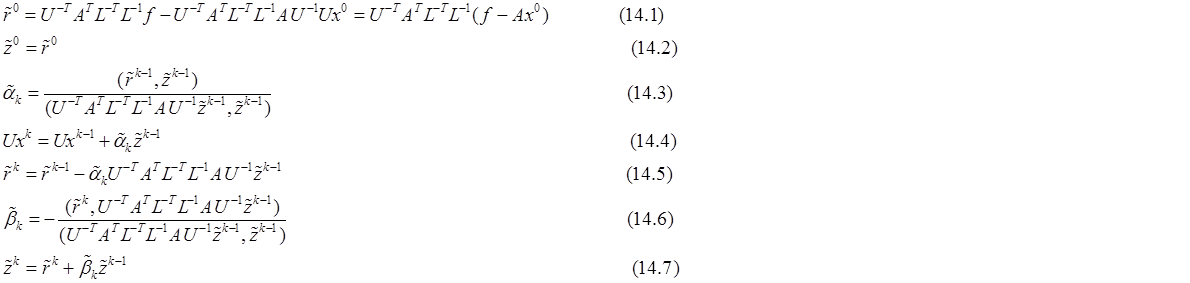Стоит отметить, что вместо вычисления вектора  удобнее вычислять вектор по формуле:

Т.е. на каждой итерации мы будем иметь решение исходной СЛАУ, а не предобусловленной. В этом случае вместо вектора нужно рекуррентно вычислять вектор  по формуле

Введем с целью минимизации вычислительных затрат вектора

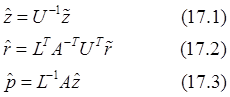
и преобразуем схему (14.1) – (14.7). Будем иметь:

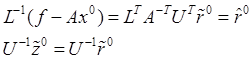
С другой стороны . Отсюда, учитывая  , получаем . Кроме того, из соотношения (17.3) находим . Преобразуем теперь итерационный процесс (14.3) – (14.7). Имеем:

. Теперь учитывая наши замены, можно записать , , . Тогда . Далее