Марковские цепи. Дискретные марковские процессы, страница 7

p(0)=(1, 0, 0, 0, 0)^T.  Запишем матрицу ^T:

.

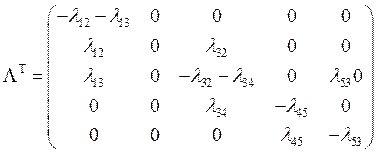
Тогда вектор p(t) является решением задачи Коши(формула 7):

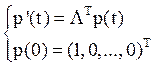.                                                                                                                 (10)

Если (t) непрерывна при t>0, то система (10) имеет единственное решение.

Если при этом матрицы (t) и 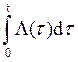 коммутативны относительно умножения при любом t, то решение задачи (10) можно записать в виде:

(11)

        6.3. Финальные вероятности

(12)

В случае конечного числа состояний ДМП существуют пределы , не зависящие от i и определённые для всех j. Это финальные вероятности системы. Уравнения для вычисления , получим, переходя в уравнении (9) к пределу при :

        6.4. Среднее время перехода из одного состояния в другое

Пусть t_ij – среднее время перехода из состояния i в состояние j. Переходы осуществляются в случайные промежутки времени, следовательно, за время  система из состояния i в состояние j перейдёт с вероятностью p_ij() и в состояние k, отличное от j – с вероятностью p_ik(). Используем формулу для условного математического ожидания:

 

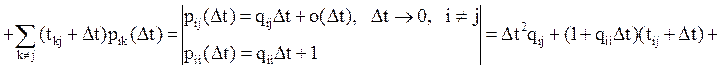
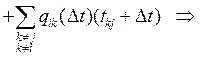 после деления обеих частей равенства на  и предельного перехода при  получаем:

(13)

Найдём ещё t_ii: , получим:

 с учётом равенства (8) получаем

t_iiq_ii=-1 или         t_ii=-1/q_ii                                                                                                       

6.5. Процесс гибели-размножения.

Так называется однородный ДМП со счётным числом состояний, когда из некоторого состояния k, k=1, 2, …, за время  возможен переход лишь в состояния k+1 и k-1; из нулевого состояния – только в первое. Такие процессы широко распространены в биологии, социологии, физике, теории массового обслуживания.

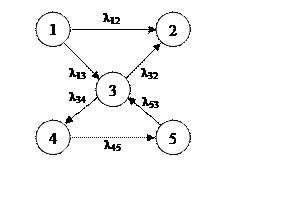
Граф состояний такого процесса имеет вид:

Для такого процесса, если существуют конечные величины q_ij, то для любого i отличны от нуля только 3 параметра – q_ii, q_i,i+1, q_i,i-1. Если ввести обозначения q_i,i+1=λ_i, q_i,i-1=μ_i, то   . Поскольку  то

Уравнения Колмогорова (6) для таких процессов с конечным числом состояний относительно финальных вероятностей  в силу того, что матрица Λ имеет вид:

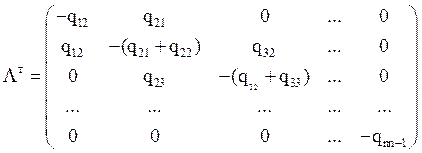, можно записать в виде:

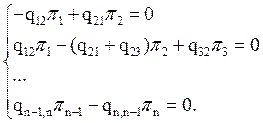.  Из первого уравнения системы получаем

_,…,.                                            

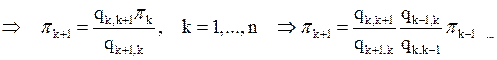           Окончательно

_.                                                                                                                                                                     

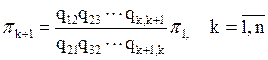Но 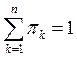, тогда

(17)

И

(18)

Или в обозначениях  получим

(19)

Здесь возможны два случая:

1) ряд 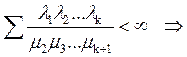 финальные вероятности существуют и равны

(24)

2) ряд 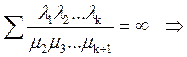 тогда =0 и финального распределения не существует. Это значит, что эволюция системы протекает в одну сторону и номер состояния всё возрастает.

Найдём t_ij – среднее время перехода из состояния i в состояние j. Система (13) приобретёт вид:

.                                                                  (20)

При  процесс гибели-размножения превращается в процесс чистого размножения. Для него уравнение (20) преобретает вид  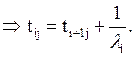Рассматриваемый процесс протекает в одну сторону, финальные  вероятности равны 0 (теорема 10, п.5.5) и t_jj=0. Тогда 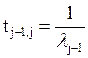. Далее, полагая i = j-2, j-3, … , получим 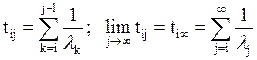 - среднее время перехода в состояние с бесконечно большим номером. Здесь опять возможны два случая:

1) 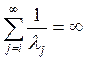, следовательно,  бесконечно большая величина, что вполне разумно.

2) 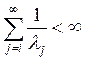, следовательно, число  - конечное. Что это может означать? Возникает лавинообразный процесс, «взрыв», эпидемия в биологический системах.