![]()
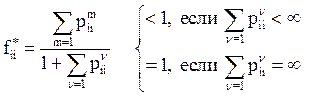
Теорема 5. Если ![]() и одно из состояний возвратно, то и другое
возвратно.
и одно из состояний возвратно, то и другое
возвратно.
Доказательство.
Пусть ![]() , тогда существуют целые числа m и l такие, что
, тогда существуют целые числа m и l такие, что ![]() и
и ![]() .
Пусть i – возвратное
состояние. Рассмотрим
.
Пусть i – возвратное
состояние. Рассмотрим ![]() . Суммируя по
. Суммируя по ![]() имеем:
имеем:
![]() или
или ![]() . Но ряд в правой части полученного
неравенства по теореме 4 расходится, но тогда расходится и ряд в левой части
. Но ряд в правой части полученного
неравенства по теореме 4 расходится, но тогда расходится и ряд в левой части ![]() по теореме 4 состояние j возвратно.
по теореме 4 состояние j возвратно.
Теорема 6. Если ![]() и состояние i
возвратно, то
и состояние i
возвратно, то ![]() .
.
Доказательство.
Повторяя рассуждения теоремы 3 можем записать ![]() .
Переходя к пределу при
.
Переходя к пределу при ![]() получаем
получаем ![]() .
По теореме 5 j – возвратное состояние
.
По теореме 5 j – возвратное состояние ![]()
![]() . Кроме того,
. Кроме того, ![]() по определению этой вероятности и условия,
что j возвратно. Но тогда
по определению этой вероятности и условия,
что j возвратно. Но тогда ![]() .
.
Теорема 7. Если состояние
i невозвратно, то ![]() .
.
Доказательство.
По формуле полной вероятности запишем ![]()
![]() . Ряд в правой части равенства
сходится
. Ряд в правой части равенства
сходится ![]()
![]() , поскольку сходится ряд
и в левой части равенства.
, поскольку сходится ряд
и в левой части равенства.
Следствие. Несущественное состояние невозвратно.
Теорема 8. Все состояние неприводимой апериодической системы возвратны.
Доказательство. Проведём доказательство методом «от противного». Предположим что все состояния такого класса невозвратны. В силу конечности числа состояний по теореме 7 имеем:
![]() . Из
этого противоречия следует, что все состояния системы не могут быть
невозвратными. Пусть i0 – возвратно, а j – произвольное состояние. Но i0
. Из
этого противоречия следует, что все состояния системы не могут быть
невозвратными. Пусть i0 – возвратно, а j – произвольное состояние. Но i0![]() j, и по теореме 5 j – возвратно.
j, и по теореме 5 j – возвратно.
Невозвратные состояния в такой системе возможны, если число состояний бесконечно.
Теорема 9.
Для апериодического неприводимого класса с конечным числом состояний для любого
состояния j существует ![]() , не
зависящий от i. Этот предел
, не
зависящий от i. Этот предел ![]() носит
название финальной вероятности состояния j.
носит
название финальной вероятности состояния j.
Доказательство теоремы довольно громоздко и не будет рассматриваться в рамках курса.
Финальные вероятности определяют вероятность при бесконечно долгом блуждании и не зависят от того, из какого состояния система начала свою эволюцию. Для стационарной цепи Маркова финальные вероятности не меняются со временем, поэтому можно сказать, что они определяют стационарное распределение вероятностей по состояниям системы. Финальные вероятности – наиболее важные характеристики марковских цепей.
В классе с
бесконечным числом состояний финальные вероятности существуют, если для всех i ![]() .
.
Теорема 10.
Пусть для марковской цепи со счётным множеством состояний и матрицей Р для всех
состояний j существуют
финальные вероятности ![]() . Тогда:
. Тогда:
а) ![]()
б) ![]() или
все
или
все ![]() =0.
=0.
Все ![]() однозначно
определяются условиями а) и б).
однозначно
определяются условиями а) и б).
Если ![]() =0 для всех i, то
соответствующий класс называется возвратным нулевым. В таком классе процесс
протекает в одном направлении, в нем не устанавливается стационарного
распределения вероятностей по состояниям. Если
=0 для всех i, то
соответствующий класс называется возвратным нулевым. В таком классе процесс
протекает в одном направлении, в нем не устанавливается стационарного
распределения вероятностей по состояниям. Если ![]() , то
соответствующий класс называется возвратным или положительно возвратным.
, то
соответствующий класс называется возвратным или положительно возвратным.
Пример 12. Для марковской цепи с матрицей переходных вероятностей вида
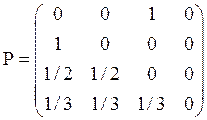 определить классы эквивалентности и
периоды состояний.
определить классы эквивалентности и
периоды состояний.
Построим граф состояний.
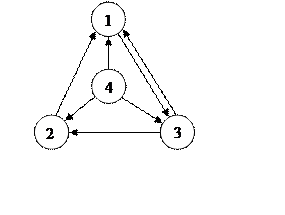
M1 = {2,3} =>d1 = 1
M2 = {3,5…} =>d2 = 1
M3 = {2,1} =>d3 = 1
M4 =
![]() =>d4
= 0
=>d4
= 0
Матрицу Р и граф состояний можно
представить иначе, для чего переобозначим состояния: ![]() .
Тогда матрица Р примет вид:
.
Тогда матрица Р примет вид:
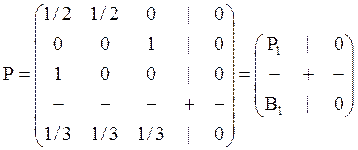 , соответствующий граф состояний
выглядит следующим образом:
, соответствующий граф состояний
выглядит следующим образом:
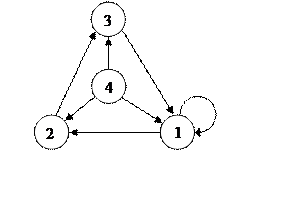
M1 = {1, 3, …} => d1 = 1
M2 = {3, 4, 5, …} => d2 = 1
M3 = {3, 4, 5, …} => d3 = 1
d4 = 0 по-прежнему.
Следовательно, существенные состояния образуют один неприводимый апериодический класс, период всех состояний равен 1.
Пример 13. Матрица Р имеет
вид: 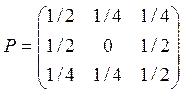 . Найти
. Найти ![]()
Для нахождения вектора ![]() решаем систему (см. теорему 10):
решаем систему (см. теорему 10): 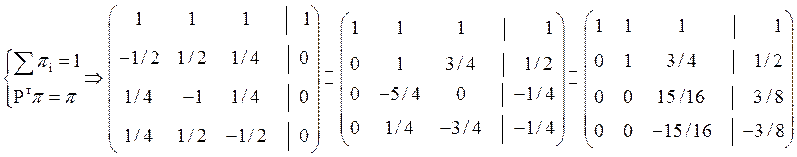
=> ![]() .
.
![]() , так как
финальные вероятности не зависят от того, из какого состояния система начинает
эволюцию).
, так как
финальные вероятности не зависят от того, из какого состояния система начинает
эволюцию).
5.6. Среднее время перехода из несущественного состояния в апериодический класс
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.