Марковские цепи. Дискретные марковские процессы, страница 5

Пусть S_k – множество состояний k-го апериодического неприводимого класса, M – множество несущественных состояний, m_i – среднее время перехода из i-го состояния, , в

k-й апериодический класс. Найдём это время.

Система из состояния i может перейти за один шаг в состояния  с вероятностью . Тогда время перехода равно 1. Если же за первый шаг система перейдёт из состояния i в некоторое состояние с вероятностью p_il, и только потом перейдёт в класс S_k, то среднее время перехода будет (1+m_l). Окончательно имеем:

. Перепишем полученное равенство в матричной форме, для чего введём обозначения: m^T=(m₁, …, m_k), e^T=(1, 1, …, 1), R=(p_ij, ). Тогда m=e+Rm, т.к. в этом случае . Следовательно,

m=(I-R)^-1e.                                                                              (7)

Так, в примере 12 всего одно несущественное состояние, поэтому m – скалярная величина, R = 0, следовательно, m = 1.

5.7. Среднее время перехода из состояния в состояние внутри класса

Пусть i и j – некоторые состояния класса S. Через m_ij обозначим среднее время перехода из i-го состояния в j-е. Если за один шаг система перейдёт в j-е состояние из i-го с вероятностью p_ij, то время перехода равно 1. Время перехода будет равно 1+m_lj, если за первый шаг система перейдёт в состояние l+j, а уж затем перейдёт в состояние j. Тогда по формуле условного математического ожидания имеем:

 или

Полученное равенство запишем в матричном виде. Пусть M={m_ij, },,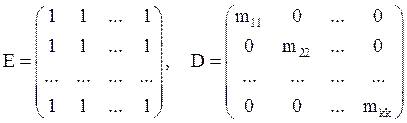 где k – число состояний данного класса S. Тогда

M = E + PM – PD

(8)

Укажем на связь чисел m_ll, , с финальными вероятностями. Для этого уравнение (8) в алгебраической форме умножим на  и просуммируем по i:

 

=1 или

(9)

Равенство (9) означает, что среднее время возвращения в положительное возвратное состояние конечно, а в нулевое возвратное состояние – бесконечно. В [3] доказывается, что уравнение (8) имеет единственное решение, определяемое формулой

M = (I – Z + E Zdg)D

(10)

где E, D – в обозначениях формулы (8), а Z = (I – P + A)^-1, где все строки матрицы А совпадают и равны вектору .

Так, в примере 13 все состояния в МЦ возвратные и можно сосчитать как m_ll , l = 1, 2, 3, так и все элементы матрицы М. 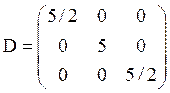. В нашем случае  ; =>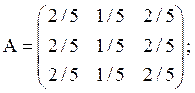

 =>

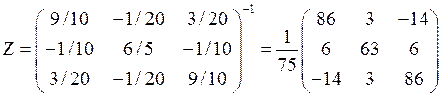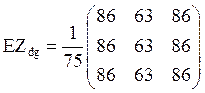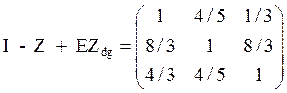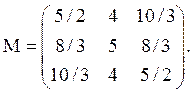
Отметим также, что если Р – переходная матрица процесса независимых испытаний (т.е. Р=А), то 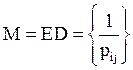 [3].

        VI. Дискретные марковские процессы

        6.1. Основные свойства

Предположим теперь, что множество значений МП – множество Х конечно или счётно, но процесс меняет свои значения в произвольные моменты времени , T – непрерывное множество. Такие МП называются дискретными марковскими процессами (ДМП). Для них      P{x_τ = j | x_t = i, x_s = k} = P{x_τ = j | x_t = i}=p_ij(t, τ) для любых s<t<τ и k, i, j  - пространства состояний МП. Вероятности p_ij(t, τ) – это вероятности перехода из состояния i в состояние j за промежуток времени (t, τ).

Если p_ij(t, τ)= p_ij(τ-t)= p_ij(σ), σ=τ-t, то есть p_ij(σ)=P{x_τ+t = j | x_t = i}, i, j , не зависит от времени  при τ > 0, то МП называют марковским процессом со стационарными вероятностями или однородным МП, или стационарным МП. Рассмотрением именно этого типа МП мы и ограничимся в последующем изложении.

Зная матрицу P(τ) = (p_ij(τ), i, j =1, 2, …,  τ) и вектор вероятностей начальных состояний системы p(0)={p_i(0)}, i, по формуле полной вероятности можно найти вероятности состояний в любой момент времени t:

(1)

Свойства переходных вероятностей:

 1.

 2.

 3.  - уравнение Чепмена-Колмогорова для ДМП. В частности, если МП однороден, то:

pij(τ+σ)=

(2)

 4. 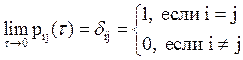 - условие стохастической непрерывности ДМП. Условие означает, что с вероятностью 1 система или процесс, описывающий эволюцию системы во времени, не изменяет своего состояния за бесконечно малый промежуток времени τ>0.