Марковские цепи. Дискретные марковские процессы

        V. Марковские цепи

    5.1. Основные определения

Определение марковской цепи (МЦ) дано в п.2.4. Это МП, пространство состояний Х которого счётно или конечно, а множество Т имеет вид {t₁, t₂, t₃,…}. Часто эти два множества Х и Т отождествляют с множеством неотрицательных целых чисел {0, 1, 2, …} и говорят, что процесс находится в состоянии k, если Х_n=k (полная форма записи ). Это делают для упрощения записи.

МЦ являются удачной математической моделью для многих реально протекающих процессов. Если некоторая техническая система S может находиться в одном из своих состояний S₁, S₂,…, S_n, к которым она переходит случайным образом в фиксированные моменты времени t₁<t₂<…, то при любом t_k система может находиться в одном из своих состояний с вероятностью p₁(t_k), p₂(t_k), …, p_n(t_k), где p_i(t_k)=P{}, - событие, состоящее в том, что система в момент времени t_k находится в состоянии S_i, . Проще эти вероятности обозначают p_i(k), заменив в них t_k на k. Тогда случайная функция X(t) – состояние системы в некоторый момент времени описывает эволюцию системы во времени и p_i(k), , - её ряд распределения в момент времени t_k.

Вектор p(k)=(p₁(k), p₂(k),…, p_n(k)) называют вектором вероятностей состояний системы в момент времени t_k или просто k. При k=0 вектор p(0)=(p₁(0), p₂(0),…, p_n(0))называют вектором вероятностей начальных состояний или начальным распределением случайной величины Х(0)≡Х₀.

Обозначим через р_ij(k) вероятность случайной величины Х_k попасть в состояние j при условии, что Х_k-1 находится в состоянии i, т.е. р_ij(k)=P{X_k=j|X_k-1=i}. Вероятности р_ij(k) называют вероятностями перехода из i-го состояния в j-е за один шаг. Наличие аргумента k означает, что эти вероятности зависят не только от состояний i и j, но и от момента осуществления перехода t_k. Если , то МЦ называется однородной.

Обычно вероятности р_ij объединяются в матрицу P:

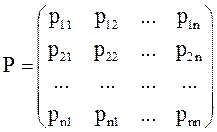, которую называют марковской матрицей или матрицей переходных вероятностей или просто переходной матрицей. В матрице n строк и столько же столбцов, равное числу состояний системы. Каждая строка матрицы представляет собой  распределение вероятностей  с. величины Х_k при условии, что  = i, i,j=. Oчевидно, что элементы матрицы Р удовлетворяют условиям:

Процесс полностью определён, если заданы матрица Р и вектор p(0). Иногда для описания МЦ используют графы состояний или размеченные графы состояний для однородной цепи.

Пример 1. Пусть дискретная случайная величина ξ принимает неотрицательные целочисленные значения с вероятностями  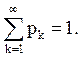Пусть далее  результаты независимых  наблюдений с. величины ξ , то есть  имеем последовательность независимых с. величин. Определим процесс , положив Матрица переходных вероятностей  для процесса имеет вид .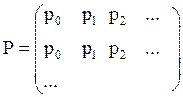

Пример 2. Определим в условиях предыдущей задачи процесс  так:.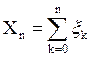

Нетрудно показать, что процесс - марковский. Действительно,  =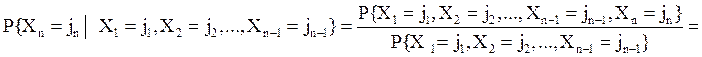

=

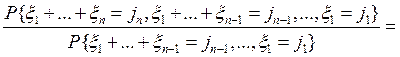
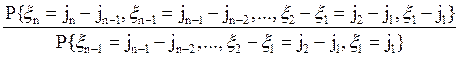
Вычисления также позволяют найти переходные вероятности 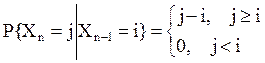. Тогд матрица переходных вероятностей выглядит следующим образом .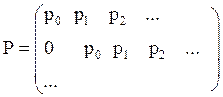

Анализ МЦ связан, главным образом, с вычислением вероятностей возможных её реализаций, важнейшей характеристикой которых является матрица вероятностей переходов за n шагов – P⁽ⁿ⁾. Элемент матрицы P⁽ⁿ⁾ – означает вероятность того, что за n шагов процесс перейдёт из состояния i в состояние j, p_ij⁽ⁿ⁾=P{X_m+n=j|X_m=i}.

Теорема 1. Если Р – матрица одношаговых переходных вероятностей МЦ, то

для любой пары фиксированных неотрицательных чисел r и s таких, что r+s=n. При этом по определению:

В формуле (2) нетрудно заметить формулу умножения матриц, поэтому P⁽ⁿ⁾= Pⁿ.

Доказательство. Пусть n=2. Событие, состоящее в переходе за 2 шага из состояния i в состояние j, может произойти одним из следующих путей: на первом шаге переход в какое-либо промежуточное состояние , а на втором шаге – из k-го состояния в j-е. Поскольку процесс марковский, то вероятности первого шага р_ik, второго - р_kj. По формуле полной вероятности имеем .

Рассуждения при n>2 аналогичны. Равенство (2) носит название  равенства  Чепмена-Колмогорова для марковских цепей. Его часто записывают в виде .

Формулу (2) можно записать и в матричной форме: P^m+n= PⁿP^m =.               (2’)

Вектор вероятностей состояний p(m+l)=p^T(m)P                                                 (4)

Здесь p(m+l)=(p₁(m+l), …, p_n(m+l)), p(m)=(p₁(m), …, p_n(m)). В частности, p(m+1)=p^T(m)P=p^T(0)P^m+1.

Равенство (4) может быть доказано также с помощью формулы полной вероятности.