Марковские цепи. Дискретные марковские процессы, страница 6

Стохастическая непрерывность МП не означает непрерывности его реализаций. В случае ДНП это совершенно очевидно, т.к. множество состояний системы дискретно, а это означает, что реализации ДНП разрывны, а сам же процесс стохастически непрерывен. Это можно пояснить тем, что разрывы реализаций происходят в случайные моменты времени и вероятность того, что разрыв произойдёт именно в точке t, равна нулю.

Матрицу Р со свойствами 1 – 4 часто называют стандартной. Из этих свойств можно получить много полезных следствий.

Теорема 1. Для однородного МП p_ij(t) равномерно непрерывны по t.

Доказательство. Условие 4) говорит о непрерывности Р в точке 0: Р(0)=I. Покажем, что P(t) непрерывна при всех t > 0. Рассмотрим  (по свойствам 3 и 4). С другой стороны при t > 0 и 0 < h < t равенство (2) можно записать в виде: P(t)=P(t-h)P(h). При малых h, P(h) существует и близка к I, тогда обратная матрица P^-1(h) существует и также близка к I. Следовательно, . Полученные соотношения показывают, что матрица P(t) непрерывна по t. При t - ограниченного замкнутого множества P(t) будет и равномерно непрерывной на Т (теорема Кантора).

Теорема 2. Для всех i.

Доказательство. По свойству 4 p_ii(0)>0. В силу стохастической непрерывности процесса существует h>0, что .

Пусть теперь t – любое из T. Тогда существует такое целое n, что 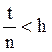 и, согласно сказанному выше, .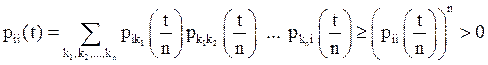

Теорема 3. Если для некоторого t₀  p_ij(t₀)>0, то .

Доказательство. Справедливость утверждения следует из свойства 3:

.

Теорема 4. Для ДМП со счётным числом состояний существуют пределы:

(3)

при этом .

Величины q_i и q_ij, ij, имеют смысл плотности (интенсивности) вероятности перехода из состояния i в состояние j за промежуток времени h>0: . Эти величины называются инфинитезимальными параметрами.

В случае конечного числа состояний системы равенство q_i = не может иметь места:

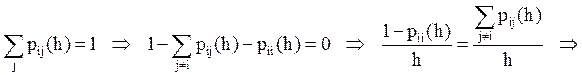
(4)

6.2. Уравнения Колмогорова

Запишем оба предела в формуле (3) в матричной форме:

(5)

Можно показать , что условие однородности дискретного марковского процесса  эквивалентно условию , что следует  из соотношений

Матрица , определяемая равенством (5), позволяет получить выражение для вычисления вероятностей p_ij(t). Для этого рассмотрим выражение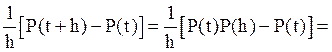

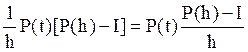. Предел правой части равенства при  существует, но тогда существует и предел левой части равенства:

(t)=P(t)= P(t).

(6)

и - матрица с элементами

Уравнение (6) носит название дифференциального уравнения Колмогорова. Его можно решать стандартными методами теории обыкновенных дифференциальных уравнений (ОДУ) при начальном условии P(0)=I. Из уравнения (6) может быть получено выражение для вектора вероятностей состояний  или

                                                                                               (7)

Уравнение (6) записано для однородного ДМП. В общем виде это уравнение принимает вид: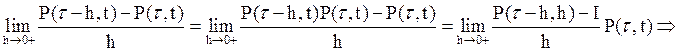

                                                                                    (8)

Здесь элементами матрицы  являются производные по τ элементы матрицы P(τ,t):

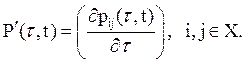
Равенство (8) называют обратной системой дифференциальных уравнений Колмогорова. Вероятность перехода определяется в момент τ<t. Или же:

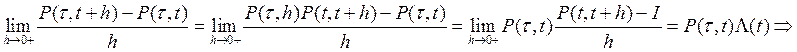
(9)

Здесь 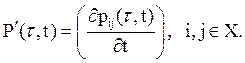  Это прямая система дифференциальных уравнений Колмогорова.

При начальных условиях P(0)=I системы (8), (9) имеют единственные решения. Если число состояний системы конечно, то решения систем (8) и (9) совпадают. При счётном множестве состояний целесообразнее решать систему (8) хотя бы потому, что при  любая МЦ удовлетворяет этой системе уравнений.

 Пример 14. На рисунке представлен размеченный граф состояний системы, процесс изменения состояния которой представляет собой однородный ДМП. Пусть T=[0,∞) и начальное состояние системы x₀=1. Иначе говоря, вектор вероятностей начальных состояний имеет вид: